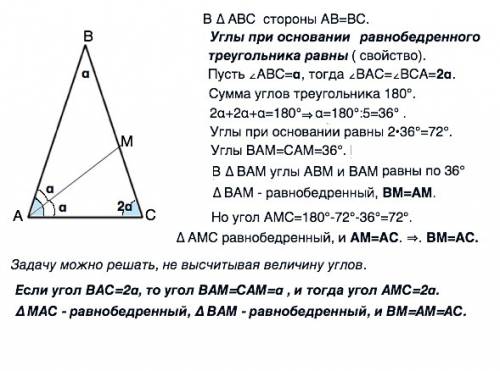
В ∆ АВС стороны АВ=ВС. Углы при основании равнобедренного треугольника равны ( свойство).
Пусть ∠АВС=α, тогда ∠ВАС=∠ВСА=2α.
Сумма углов треугольника 180°. 2α+2α+α=180° α=180°:5=36° .
Углы при основании равны 2•36°=72°.
Углы ВАМ=САМ=36°. В ∆ ВАМ углы АВМ и ВАМ равны по 36°.
∆ ВАМ - равнобедренный, ВМ=АМ.
Но угол АМС=180°-72°-36°=72°.
∆ АМС равнобедренный, и АМ=АС. ⇒. ВМ=АС.
-------
Задачу можно решать, не высчитывая величину углов.
Если угол ВАС=2α, то угол ВАМ=САМ=α , и тогда угол АМС=2α.
∆ МАС - равнобедренный, ∆ ВАМ - равнобедренный, и ВМ=АМ=АС.
1.
Нарисовать окружность. Разделить ее радиусом на 6 частей. Две точки соединить с центром окружности. Соединить хордой концы раюиусов на окружности. Хорду обычным путем разделить на две равные части. Соединить с центром окружности.
2.
Можно построить прямой угол, проведя обычным перпендикуляр к прямой. Отложить на одной из сторон какой-то отрезок. Затем из свободного конца этого отрезка провести окружность радиусом больше того отрезка в два раза.
Точку пересечения окружности со второй стороной прямого угла соединить с концом первого отрезка. Получим треугольник с катетом длиной вдвое меньшей длины гипотенузы. Угол, лежащий против такого катета, будет равен 30 градусам.