BC = 16/(2√3 - 1) см.
Объяснение:
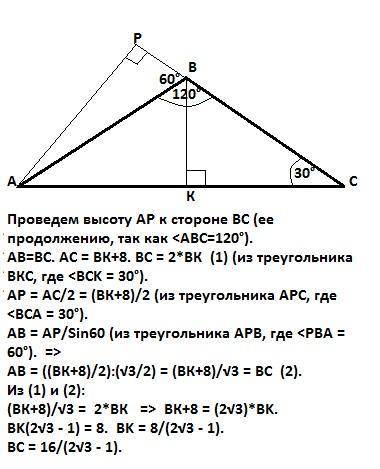
Треугольник АВС равнобедренный, медиана ВК является и высотой, и биссектрисой. (см. рисунок в задании).
Проведем высоту АР к стороне ВС (ее продолжению, так как ∠<ABC=120°), АВ=ВС, АС = ВК+8см (дано).
ВС = 2*ВК (1) (из треугольника ВКС, где ∠BKC=90°, a ∠BCK=30°).
АР = АС/2 = (ВК+8)/2 (из треугольника АРС где ∠APC=90°, a ∠BCA=30°).
АВ = АР/Sin60 (из треугольника АРB, где ∠APB=90°, a ∠РBA=60°, а
Sin(∠PBA = AP/AB). Sin60 = √3/2 =>
АВ = ((ВК+8)/2):(√3/2) = (ВК+8)/√3 = ВС (2).
Из (1) и (2):
(ВК+8)/√3 = 2*ВК => ВК+8 = (2√3)*BK.
BK(2√3 - 1) = 8. BK = 8/(2√3 - 1).
BC = 16/(2√3 - 1)см.
a^2=b*h,
8^2=4b
4b=64
b=16
ответ: 16