Объяснение:
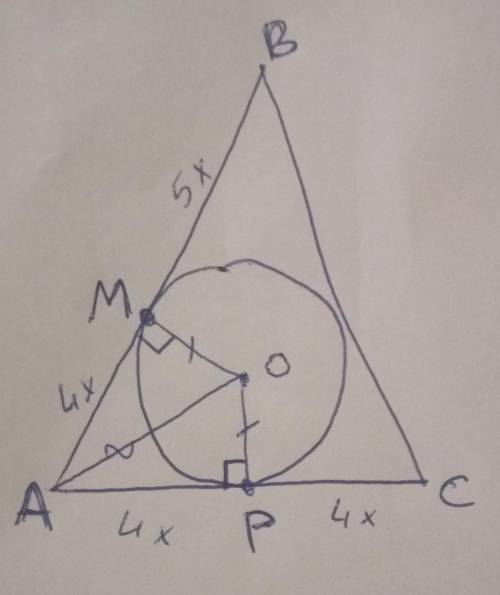
Уявімо собі трикутник АВС з основою АС, вписане коло з центром О. Ця окружність буде стосуватися до сторони АВ в точці М, а до основи АС в точці Р. За умовами - АМ: МВ = 4: 5
Периметр трикутника: P=AB+BC+AC=52
Розглянемо трикутники АМО і АРО:
Кути М=Р=90 (це радіуси кола), отже ОМ=ОР, АО - загальна сторона.
Отже трикутник АМО=АРО і отже АР=АМ АР:МВ=4:5
Визначимо одиницю пропорції як х, тобто АР:МВ=4:5=4х:5х
AB=BC=4x+5x за умовами
AC=4x+4х
2(4x+5x)+(4x+4x)=52
8x+10x+8x=52
26x=52
x=2
AB=BC=4*2+5*2=18
AC=4*2+4*2=16
1. Дано: прямΔАВС с гипотенузой АВ; АВ=10, ∠СВА=60°;
Найти: ВС-?
Решение: ∠ВАС=90°-60°=30°, ВС - катет, лежащий против угла в 30°, он равен половине гипотенузы ВА, т.е. 5.
ответ: 5.
2. Дано: прямΔАВС с гипотенузой АВ; ∠АВС=45°, высота СD=8;
Найти: АВ-?
Решение: ΔАВС р/б, ∠САВ=45° (90°-45°); высота CD является медианой для гипотенузы АВ. По свойству, CD=1/2АВ. Т.е. АВ=16.
ответ: 16.
3. Дано: прямΔАВС с гипотенузой АВ; ∠ВАС=30°;
mЕ∈АС, ∠ВЕС=60°, ЕС=7;
Найти: АЕ-?
Решение: ∠ЕВС=90°-60°=30°, ЕС - катет, лежащий против угла в 30°, он равен половине гипотенузы ВЕ, т.е. ВЕ=14. ∠АВС=90°-∠ВАС=60°. Т.е. ∠АВЕ=60°-∠ЕВС=30°, ⇒ ΔАВЕ р/б, т.к. ∠ВАЕ=∠АВЕ, ⇒АЕ=ВЕ=14.
ответ: 14.
4. Дано: р/б ΔАВD с основанием ВD, АС - высота, CD=3.5см;
Найти: ∠В и ∠С;
Решение: АС⊥ВD, значит ∠ВСА=90°. АС является медианой для ВD, т.к. проведена к основанию, ⇒ ВС=3.5. АВ=1/2ВС, ⇒ ∠ВАС=30°, ⇒ ∠АВС=90°-30°=60°.
ответ: 60°, 90°.
5. Дано: прямΔРКЕ с гипотенузой РЕ; внеш.уг. при вершине Р=150°; КЕ=9; КС-высота;
Найти: РС и СЕ;
Решение: ∠КЕР=150°-90°=60° (св-во внеш. уг.); ∠СКЕ=90°-60°=30°, ⇒ СЕ - катет, лежащий против угла в 30°, он равен половине гипотенузы КЕ, ⇒ СЕ=9:2=4.5. ∠КРЕ=180°-150°=30° (смеж.уг.); КЕ - катет, лежащий против угла в 30°, он равен половине гипотенузы РЕ, ⇒ 9*2=18. РЕ=РС+СЕ, ⇒ РС=18-4.5=13.5.
ответ: 13.5 - РС, 4.5 - СЕ.
6. Дано: прямΔСАВ с гипотенузой АВ; внеш. уг. при вершине В=150°; АА₁-биссектриса ∠САВ; АА₁=20;
Найти: СА₁;
Решение: ∠САВ=150°-90°=60° (св-во внеш. уг.); ∠САА₁=1/2∠САВ, ⇒ ∠САА₁=60°:2=30°; СА₁ - катет, лежащий против угла в 30°, он равен половине гипотенузы АА₁, ⇒ СА₁=20:2=10.
ответ: 10.
Фото
Объяснение: