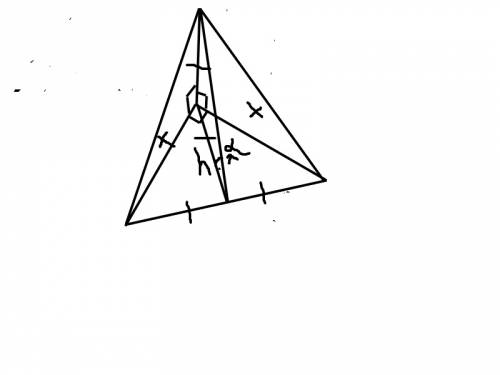
а)зная гипотенузу найдем катеты..по теореме пифагора: a²+b² = c² (a = b = х)
2х² = 32, х = √16 = 4.
теперь найдем высоту основания:
h ² = 16 - 8 = √8
так как угол α = 45 , то h основания = h пирамиды = ребро = √8. 1-е ребро
2-е и 3 -е найдем так же по теореме пифагора:
l = √16+8 = √24
б) S бок = S1 + S2 + S3
S1 = √8 * 4 /2 = 2√8 = 4√2 (S грани, прямоуголный треугольник)
S2 = √8 * 4 /2 = 2√8 = 4√2 (S грани, прямоуголный треугольник)
S3 = 4 * 4√2/2 = 8√2 (S грани, равнобедренный треугольник)
S = 16√2
Эта задача решается сама собой, если представить такой ромб, как составленный из 2 равностороних треугольников.
Сраз ясно, что высоты ромба (вот эти самые перпендикуляры) равны 6. (Каждый из этих перпендикуляров - высота в правильном треугольнике, и приходит в середину соседних сторон ромба, поэтому расстояние между концами - это половина большой диагонали (средняя линяя!), которая (БОЛЬШАЯ ДИАГОНАЛЬ РОМБА!, в свою очередь) составлена из 2 таких высот правильного треугольника :)))
Итак, высота ромба 6. Значит сторона 6/(корень(3)/2) = 4*корень(3). А периметр
16*корень(3).
Это повтор такого же моего решения... :))) Я предполагаю, что соотношение между стороной правильного треугольника и его высотой вам известно.
Это h = a*корень(3)/2. Его легко получить из простой теоремы Пифагора для треугольника с гипотенузой 2 и катетом 1 (это как бы половина правильного треугольника). Второй катет будет корень(3), а отношение к гипотенузе - корень(3)/2 (само собой, это справделиво ДЛЯ ЛЮБОГО правильного треугольника, они все между собой подобны).
V = Sосн* h
1) Найдем S осн. Основание АBCD - ромб, периметр которого 40 см => сторона ромба a равна 40 : 4 = 10 см. Одна из диагоналей ромба равна 12 см, и диагонали ромба перпендикулярны и делятся точкой пересечения пополам, значит если обозначить пересечение диагоналей т.О, то получим четыре равных прямоугольных треугольника. Рассмортим один из них - АОВ. В нем гипотенуза равна a = 10 см, а один из катетов, например, АО = 12:2 = 6 см. Найдем по т. Пифагора другой катет ВО = √(10² - 6²) = √(100 - 36) = √64 = 8 см.
Тогда площадь треугольника АОВ равна S(АОВ) = АО*ВО /2 = 6*8 /2 = 24 см²,
а площадь всего основания прямого параллелепипеда
S осн = 4* S(АОВ) = 4*24 = 96 см².
2) Найдем высоту h прямого параллелепипеда.
По условию нам известна его диагональ d = 20 см.
Т.к. в основании прямого параллелепипеда лежит ромб, то это может быть как большая, так и меньшая диагональ.
Пусть она соответсвует диагонали ромба 12 см, тогда высота параллелепипеда будет равна: h = √(20² - 12²) =√(400 - 144) = √256 = 16
и V = Sосн * h = 96 * 16 = 1536 см³
Если же она соответсвует диагонали ромба 16 см, тогда высота параллелепипеда будет равна: h = √(20² - 16²) =√(400 - 256) = √144 = 12
и V = Sосн * h = 96 * 12 = 1152 см³
ответ: 1152 см³ или 1536 см³