Ребята сделайте со всеми решениями
даю
1.
Вершины треугольника ABC лежат на окружности, центр окружности O лежит внутри треугольника. Дуги AC и BC относятся как 7:8, ∠C=30∘.Определи величины углов B;A;AOC.
∠B=
∠A=
∠AOC=
2.
Хорды окружности AB и CM пересекаются в точке K так, что AK=BK. Вычисли длину AB, если CK=8 и CK:KM=4:1.
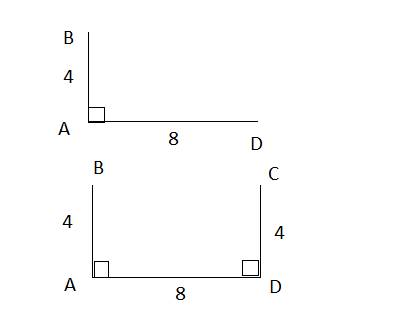

BD=CD по условию, а ED - общий катет. Отсюда ∠BDE=∠CDE,
а т.к. точки A,D,E лежат на одной прямой, то и ∠BDA=∠CDA.
(Заметим, что если Е совпала с D, то равенство углов ∠BDA и ∠CDA следует сразу из условия, т.к. BC⊥AD).
Далее, треугольники BDA и CDA равны по сторонам и углу между ними
(AD - общая, BD=CD по условию, ∠BDA=∠CDA доказали выше), а значит, AB=AC, что и требовалось.