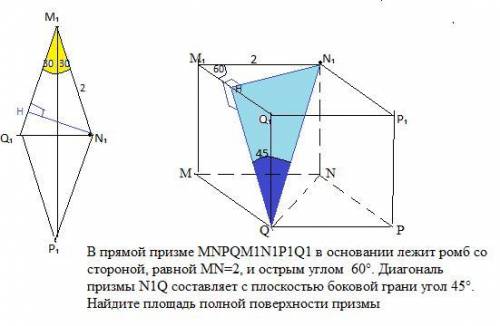
"В прямой призме MNPQM1N1P1Q1 в основании лежит ромб со стороной, равной MN=2, и острым углом ∠ = 60°. Диагональ призмы N1Q составляет с плоскостью боковой грани угол 45°. Найдите площадь полной поверхности призмы "
Объяснение:
1)S(полн.призмы)=2S(осн)+S(бок)
S(осн)=S( ромба)=а²*sinα, где а-сторона основания ,α-угол между сторонами.
S(бок)=Р(осн)*h , где h-высота призмы, в прямой призме боковое ребро.
2) S(осн)=S(ромба)=2²*sin60°=4*√3/2=2√3 (ед²)
3) Чтобы найти S(бок), надо найти боковое ребро NN₁ из прямоугольного ΔQNN₁. Для этого надо знать
1) QN → из ΔQ₁N₁М₁-равносторонний ,т.к
∠Q₁N₁М₁=60° , Q₁N₁=QN=2 ;
2) QN₁. из ΔQN₁H- прямоугольный (cм*),
sin45°= N₁H/ QN₁ (**) ,
√2/2=√3/ QN₁ , QN₁ = 2√3/√2=√3*√2=√6
ΔQN N₁-прямоугольный , по т. Пифагора
NN₁=√( QN₁²- QN²)=√(√6²- 2²)=√2.
4)S(бок)=(2*4)*√2=8√2(ед²)
S(полн.призмы)=2*2√3+8√2=4√3+8√2
///////////////////
Вычисления и обоснования:
(*) Пусть N₁H ⊥M₁Q₁ , тогда QH ⊥ M₁Q₁ по т. о трех перпендикулярах и углом между диагональю призмы и плоскостью боковой грани будет ∠N₁QH=45°.
(**)ΔM₁Q₁Н – прямоугольный , sin60°= N₁H/ N₁M₁ ,
√3/2= N₁H/2 , N₁H=√3.
Понадобятся :
циркуль, линейка, угольник с прямым углом для построения параллельных прямых, транспортир, карандаш.
1). Чертим окружность данного радиуса.
2).Под ней чертим произвольную прямую с точкой касания с окружностью в точке Н.
3). От Н вправо откладываем НК, приближенно равную по длине данной стороне.
4). От К как от вершины строим данный угол с транспортира ( или по методике построения угла)
5). Из центра О проводим к этой стороне угла перпендикуляр ОТ по стандартному методу.
6). Через точку пересечения ОТ и окружности проводим параллельно КТ касательную к окружности. Точку ее пересечения с прямой НК обозначим А. Это вершина угла заданной величины.
7). От А откладываем длину данной стороны. Ставим точку В. ВН по свойству касательной из одной точки равен длине отрезка от В до точки касания окружности с третьей стороной.
8). Раствором циркуля, равным ВН, проводим из В, как из центра, полуокружность до пересечения с окружностью в точке Е.
9). Из В через т.Е проводим касательную до пересечения с прямой, проведенной из вершины А, т.е. со второй стороной угла А. Точка пересечения С будет третьей вершиной треугольника.
Треугольник АВС построен.