252 ед².
Объяснение:
В равностороннем треугольнике стороны равны, а все углы по 60°.
ВА = ВС = АС = 18:3 = 6 ед.
Вектор (ВС - 3ВА)² - это квадрат модуля вектора |ВС - 3ВА|.
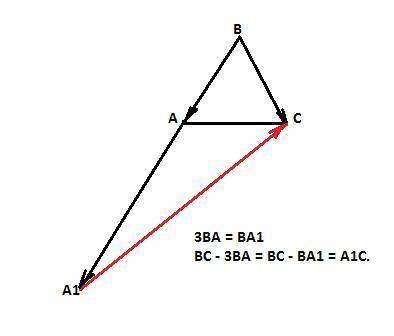
Вектор 3ВА= ВА1 = 18 ед. (равен трем коллинеарным векторам ВА, расположенным на одной прямой, конец которого будет в точке А1).
По правилу вычитания векторов имеем:
ВС - 3ВА = ВС - ВА1 = А1С.
Вектор А1С² находим по теореме косинусов:
|A1С|² = |BC|² + |BA1|² - 2|BC|·|BA1|·Cos60 =>
|A1С|² = |6|² + |18|² - 2·6·18·(1/2) = 252 ед.
Но А1С² это как раз искомый вектор.
Дано:
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.
Полная площадь такой пирамиды состоит из площадей 4-х прямоугольных треугольников, образующих её поверхность. Найдем площадь основания АВС. Здесь АС и ВС - катеты, т.к. они меньше АВ. Sосн.=3*4/2=6.
Треугольник ДАВ - прямоугольный с катетами АВ и ДА. Sdab=5*4/2=10.
Треугольник ДАС - прямоугольный с катетами АС и ДА. Sdaс=3*4/2=6.
Треугольник ДСВ - прямоугольный с катетами ВС и ДС. Т.к. ДС - гипотенуза в треугольнике ДАС, то
Sdсb=5*4/2=10.
Итого, площадь поверхности пирамиды ДАВС=6+10+6+10=32.