
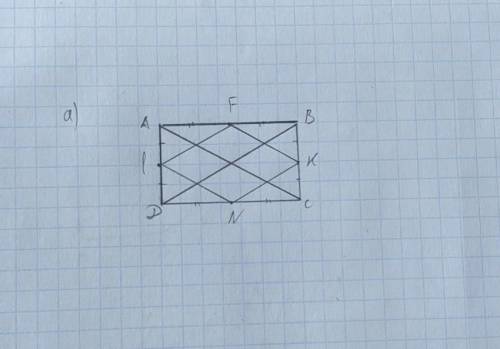
Объяснение:
a) Ромб - параллелограмм, у которого все стороны равны, а углы непрямые.
Рассмотрим ∆DAB:
LF - средняя линия треугольника, т.к AF=FB и AL=LD => LF // DB
Рассмотрим ∆BCD:
NK - средняя линия треугольника по таким же признакам, и NK // DB => и // LF.
В ∆ABC и ∆ADC FK // AC // LN по таким же признакам.
Мы знаем, что средняя линия треугольника равна половине основания этого треугольника, и по свойствам прямоугольника: AC=DB => и FK=KN=NL=LF
=> FKNL - ромб по определению. Ч.Т.Д.
б) мы можем свободно использовать равнобедренную трапецию, у которой диагонали равны, => доказательство соответствует пункту a)
углы при основании в равнобедренном треугольнике равны, обозначим их через х; тогда угол при вершине равен (18+х)°; сумма углов в треугольнике равна 180°;
Объяснение:составим уравнение: х+х+18+х=180; 3х=180-18; х=162:3=54°; углы при основании равны по 54°; угол при вершине равен 54+18=72°;