1. С точки M до плоскости квадрата ABCD проведены перпендикуляр MC и наклонную MB. Обоснуйте взаимное расположение стороны квадрата AB и плоскости MCB.
2. С точки M до плоскости треугольника ABC проведен перпендикуляр MA и наклонную MK. Обоснуйте взаимное расположение плоскости MAK и стороны BC, если AK - высота треугольника.
3. Прямая AK - касательная к окружности с центром O (K - точка соприкосновения). С точки M плоскости круга проведен перпендикуляр MO и наклонные MA и MK. Какая из этих наклонных перпендикулярна прямой AK?
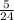г/кв ед
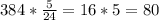грамм
СМ=МД=СД/2=5
Диагональ АС = √(АВ²+ВС²)=√2*10²=10√2
Площадь прямоугольного ΔАВС Sавс=АВ*ВС/2=10*10/2=50
Площадь прямоугольного ΔВСМ Sвсм=СМ*ВС/2=5*10/2=25
ΔАВN и ΔCNM подобны по 3 углам (<BNA=<MNC как вертикальные, <BAN=<MCN=45° (диагональ АС - биссектриса угла квадрата) и <АВN=<СМN=180-<BAN=<BNA).
Значит AN/NC=BN/NM=AB/CM=10/5=2
ΔАВN и ΔCВN имеют общую высоту из вершины В, поэтому их площади относятся как основания АN и NС
Saвn/Scвn=AN/NC=2
Saвn=2Scвn
Saвс=Saвn+Scвn=2Scвn+Scвn=3Scвn
Scвn=Sавс/3=50/3
Saвn=100/3
Площадь Sanмд=Sавсд-Saвn-Sвсм=100-100/3-25=75-100/3=125/3=41 2/3