Дано: ABCD - прямоугольная трапеция (BC||AD, AB⊥AD), окружность, впис. в ABCD, R= 4, CD = 17 см.
Найти: BC, AD.
Решение.
Проведём высоту СН.
Диаметр NK, проведённый через точки соприкосновения окружности, равен высоте СН. Также, высота и боковая сторона прямоугольной трапеции, прилежащая к прямому углу, равны. СН=NK=AB.
NK=CH=AB=d= 2R= 2•4= 8 (см).
В прямоугольном ΔCHD (∠CHD=90°) по т. Пифагора:
HD²= CD² - CH²;
HD²= 17² - 8²;
HD²= 289 - 64;
HD²= 225;
HD= 15 (-15 не подходит).
AD= AH+HD, AH=BC (поскольку AB и CH высоты), значит, AD= BC+HD => AD= BC+15.
Свойство трапеции, в которую вписана окружность:
если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.
Отсюда, BC+AD=AB+CD,
BC+ (BC+15)= 8+17;
2BC+ 15= 25;
2BC= 10;
BC= 5 (см).
Значит, AD= 5+15= 20 см.
ОТВЕТ: 5 см, 20 см.
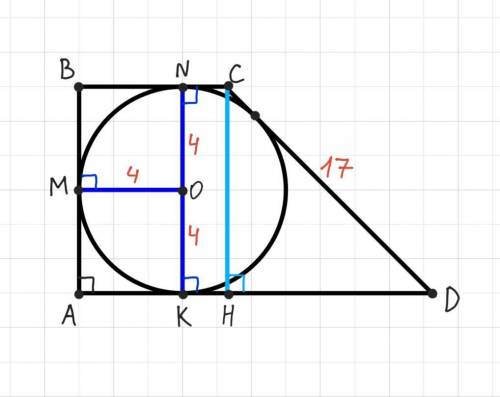
Дано: ABCD - прямоугольная трапеция (BC||AD, AB⊥AD), окружность, впис. в ABCD, R= 4, CD = 17 см.
Найти: BC, AD.
Решение.
Проведём высоту СН.
Диаметр NK, проведённый через точки соприкосновения окружности, равен высоте СН. Также, высота и боковая сторона прямоугольной трапеции, прилежащая к прямому углу, равны. СН=NK=AB.
NK=CH=AB=d= 2R= 2•4= 8 (см).
В прямоугольном ΔCHD (∠CHD=90°) по т. Пифагора:
HD²= CD² - CH²;
HD²= 17² - 8²;
HD²= 289 - 64;
HD²= 225;
HD= 15 (-15 не подходит).
AD= AH+HD, AH=BC (поскольку AB и CH высоты), значит, AD= BC+HD => AD= BC+15.
Свойство трапеции, в которую вписана окружность:
если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.
Отсюда, BC+AD=AB+CD,
BC+ (BC+15)= 8+17;
2BC+ 15= 25;
2BC= 10;
BC= 5 (см).
Значит, AD= 5+15= 20 см.
ОТВЕТ: 5 см, 20 см.

134∘
Объяснение:
MO = ON как радиусы, => треугольник MON - равнобедренный, => <NMO = <MNO = 23, => <MON = 180 - 23 - 23 =134.
∠FOK и ∠MON - вертикальные, а по свойству вертикальных углов они равны, т.е. ∠FOK = ∠MON = 134 ∘