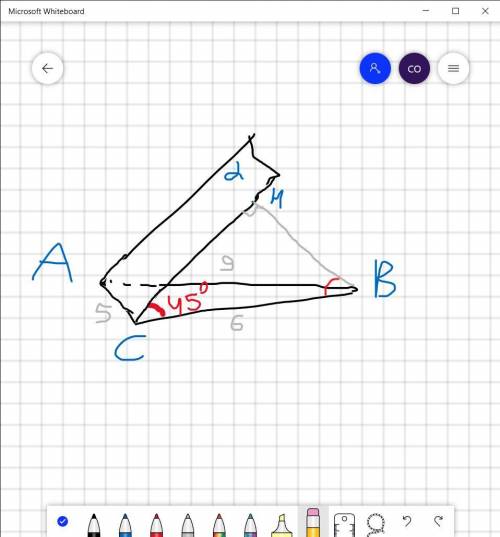
Дано: ΔABC
<(α,ABC)=45°
AB=9см ;BC = 6 см; AC = 5 см
α∩ABC =AC
BH⊥α
Знайти: BH
Розв'язання
ВС-похила до площини α, а ВН-перпендикуляр (оскільки відстань від точки до площини це перпендикуляр проведений із неї до цієї площини), тоді НС-проєкція.
Отже, проєкція похилої НС до площини трикутника ΔABC лежить на відрізку СВ => <HCB=<(α,ABC)=45°
Отримуємо прямокутний трикутник ΔВНС із прямим кутом <СНВ.
Знайдемо невідомий кут <НВС=90°-<HCB=90°-45°=45°
<HCB=<НВС, отже трикутник ΔВНС рівнобедрений і позначимо рівні сторони НС=НВ=х
За теоремою Піфагора
НС²+НВ²=СВ²
х²+х²=6²
2х²=36 | : 2
x²=18
x₁= -√18 (сторонній корень)
х₂=√18=√(9*2)=3√2 см
Відповідь: 3√2 см
(сподіваюся, що правильно)
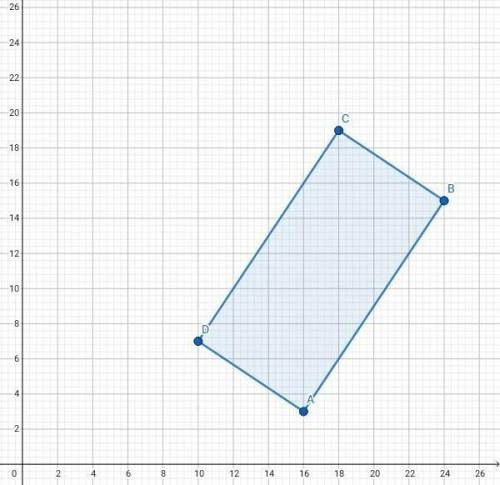
1. Вспомним признак прямоугольника: если в четырёхугольнике три угла равны по 90°, то этот четырёхугольник - прямоугольник. Рассмотрим и проверим этот признак в данной задаче:
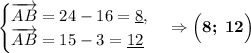
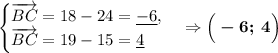
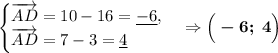
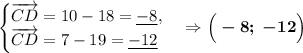
Вспомним свойство о скалярном произведении векторов: если произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны. Найдём такие пары векторов:
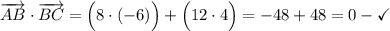
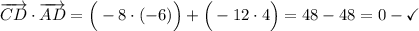
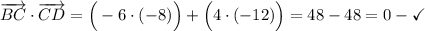
Теперь мы можем утверждать, что фигура "ABCD" - прямоугольник, т.к. углы "B", "C" и "D" составляют по 90° каждый.
Что и требовалось доказать.
2. Площадь прямоугольника - произведение его длины и ширины. Поэтому сначала нужно найти, чему равна длина и ширина.
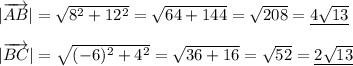
Теперь, когда нам известна и длина, и ширина, найдём площадь прямоугольника:
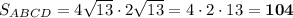 см².
см².
ответ: 104 см².
На расстоянии 3 см от центра окружности радиуса 5 см отмечена точка P. Найдите длину хорды AB,если PA= 2см