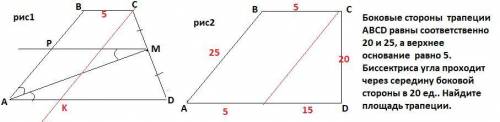
Боковые стороны трапеции ABCD равны соответственно 20 и 25, а верхнее основание равно 5. Биссектриса угла проходит через середину боковой стороны в 20 ед.. Найдите площадь трапеции.
Объяснение:
1) Пусть АВСD-трапеция, АВ=25 , ВС=5 ,СD=20 , АМ-биссектриса.
2) Проведем МК║АD ⇒ РМ-средняя линия , АР=РВ=12,5 .
Тогда ∠DАМ=∠РМА как накрест лежащие , при АМ-секущей и ∠РАМ=∠DАМ ⇒ ∠РАМ=∠РМD ⇒ ΔАМР- равнобедренный и АР=РМ=12,5.
3) По т. о средней линии трапеции РМ=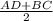
, 12,5=
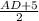,AD=20 .
4) Проведем СК║АВ , тогда АВСК-параллелограмм и СК=25.
Рассмотрим ΔКСD. Проверим т. обратную т. Пифагора :
25²=625 ; 15²+20²=225+400=625 , а 625=625 ⇒ΔКСD-прямоугольный и CD⊥AD ( см чертеж 2). Поэтому боковая сторона СD -высота.
5) S (трапеции) =1/2*h*(a+b) ; S (трапеции) =1/2*20*(20+5) =50 (ед²)
=============================
Теорема ,обратная т. Пифагора : Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
пусть авс-прямоугольный треугольник. тогда гипотенуза ас=17 см. пусть медиана выходит из точки а пусть аm — медиана(тогда bm=cm) обозначим катет bc через y, ac через x, тогда bm=cm=y\2,по теореме пифагора получаем систему и з двух уравнений первое х^2+y^2=17^2 второе x^2+(y\2)^2=15^2 отняв от первое второе получаем 3\4*(y^2)=64 y^2=256\3 y=(+\-)16\корень(3)=(+\-)16\3*корень(3) нас удовлетворяет только положительный корень(длина катета не может быть отрицательным числом), так что y=16\3*корень(3) подставив найденное значение y в первое уравнение находим х х^2+y^2=17^2 х^2+256\3=17^2 х^2=611\3 х=(+\-)корень(611\3) (нас удовлетворяет только положительное значение по той же причине что и выше) х=корень(611\3)ответ корень(611\3) и 16\3*корень(3) катеты треугольника