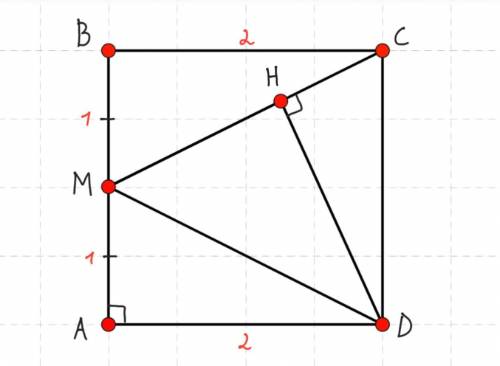
Дано: ABCD — квадрат, Sabcd= 4, т.М — середина АВ, АМ=ВМ, DH⟂СМ.
Найти: DH.
Решение.
1) Найдем сторону квадрата.
АВ²= 4;
АВ= 2 (–2 не подходит).
AB=BC=CD=AD= 2.
т.M — середина АВ, значит, АМ=ВМ= 2:2= 1.
2) Мы видим два равных прямоугольных треугольника: ΔMBC и ΔMAD (равны по двум катетам).
Найдем их площадь. Площадь прямоугольного треугольника равна половине произведения его катетов.
Значит, Smbc= Smad= ½•1•2= 1.
3) А площадь треугольника MDC равна разности площади квадрата и площадей треугольников MBC и MAD.
Т.е. Smdc= Sabcd–Smbc–Smad= 4–1–1= 4–2= 2.
4) Найдем сторону МС прямоугольного треугольника МВС (МС - это гипотенуза) по т.Пифагора:
МС²= МВ²+ВС²;
МС²= 1+2²;
МС²= 5;
МС= √5
5) Площадь обычного (произвольного) треугольника равна произведению половины основания этого треугольника на высоту, проведённую к этому основанию.
Для треугольника MDC это выглядит так:
Smdc= ½•MC•DH.
2= ½•√5•DH;
2 : ½ = √5DH;
√5DH= 4;
DH= 4/√5.
Расстояние от вершины D квадрата ABCD до прямой СМ равно 4/√5.
ОТВЕТ: 4/√5.
Доказать это просто:
1) Из каждой вершины выходит n-1 отрезок к остальным n-1 вершине.
Но к двум соседним вершинам - это стороны, а не диагонали.
Поэтому из каждой вершины выходит n-3 диагонали.
Вершин всего n, поэтому получается n*(n-3) диагоналей.
2) Каждая диагональ соединяет две вершины. Если мы провели диагональ АС, то одновременно мы провели диагональ СА.
Поэтому количество диагоналей нужно разделить пополам.
Получается d = n*(n-3)/2
1) n = 4, d = 4*1/2 = 2
2) n = 5, d = 5*2/2 = 5
3) n = 6, d = 6*3/2 = 9
4) n = 10, d = 10*7/2 = 35