По одной из формул: площадь треугольника равна половине произведения длин его сторон на синус угла между ними.
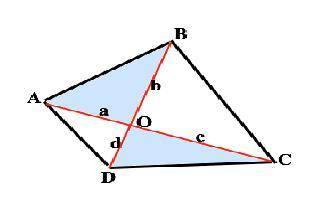
При пересечении диагоналей вертикальные углы равны.
Пусть ∠АОВ=∠DOC=α Тогда смежные им ∠DOA=∠BOC=180°- α. sinα=sin(180°- α)
Примем АО=а, ВО=b, СО=с, DO=d. Тогда:
S(AOB)=a•b•sinα/2
Ѕ(DOC)=d•c•sinα/2
S(AOB)•Ѕ(DOC)=a•b•c•d•sin²α/4
S(AOD)=a•d•sinα/2
S(BOC)=b•c•sinα /2
S(AOD)•S(BOC)=a•d•b•c•sin²α/4
a•b•c•d•sin²α/4 =a•d•b•c•sin²α/4 ⇒
S(AOB)•Ѕ(DOC)= S(AOD)•S(BOC), что и требовалось доказать.
Объяснение:
5*2=10(см)-боковые стороны равнобедренного треугольника АВС
Р=5+10+10-25см-периметр треугольника АВС