В равнобедренном треугольнике углы при основании равны.
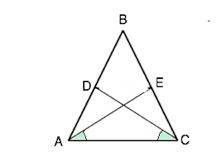
Рассмотрим ∆ ВСD и ∆ BAЕ. ∠АВС- общий.
∠ВАЕ=∠ВАС-∠САЕ,
∠ВCD=∠ВСА-∠АСD. По условию ∠ЕАС=∠DCА, ⇒ ∠ВАЕ=∠ВСD
Треугольники ВАЕ и ВСD равны по стороне ( АВ=ВС по условию) и прилежащим к ней углам (ВАЕ=ВСD, угол В - общий). Следовательно, ВD=ВЕ. Доказано.
* * *
Вариант решения- доказать равенство треугольников АСD и АСЕ по общей стороне АС и двум прилежащим углам. Тогда при вычитании из равных сторон АВ и СВ равных отрезковостанутся равные BD и ВЕ
Подобные треугольники - треугольники, углы которых соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника. То есть и площади также должны быть пропорциональны.
Посчитаем площадь одного треугольника: 2+5+6=13 см. Разделим площадь большого треугольника (26 см) на площадь маленького (13 см), получится 2. Это означает, что стороны большого треугольника в 2 раза больше сторон маленького. Рассчитаем стороны большого треугольника: 2*2=4 см, 5*2=10 см, 6*2=12 см. Проверим правильно ли мы посчитали стороны: 4+10+12=26 см - периметр. Верно.
ответ: большая сторона подобного треугольника - 12 см.