обозначим известный катет за а, а=18, угол А =30 градусам, угол С=90 градусам.
один угол прямоугольного треугольника равен 30 градусам, значит 2 угол равен 60 градусам.
Воспользуемся теоремой синусов и углом в 60 грудусов для нахождения гипотенузы(обозначим ее за с):
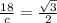
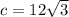
находим второй катет (б) = 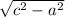 =
= 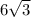
т.к. из угла в 60 градусов проводят биссектрису, каждый из образовавшихся углов равен 30 градусам. рассмотрим треугольник образовавшийся стороной б и бессектрисой к стороне а.
для нахождения гиппотенузы(искомый компоннт, обозначим за к) воспользуемся теоремой косинуса:
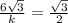
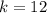
Решить, значит найти все стороны и углы этого треугольника
1) Найдем угол А: А=180-60-105=15 градусов ( по теореме о сумме углов треугольника)
2) По теореме синусов найдем АС: 7/sin15 гр=АС/ sin60 гр ( теорема: стороны треугольника пропорциональны синусам противолежащих углов)
7/0.2588=АС/0.8660 (sin 15гр и 60 гр нашли по таблице Брадиса)
АС=6.062/02588 =23.4 см
3) АВ можно найти двумя либо через теорему косинусов либо через теорему синусов. Найдем по теореме косинусов АВ2= ВС2+АС2-2АВВСcos угла С (Теорема косинусов квадрат стороны треугольника равен сумме квадратов других его сторон минус удвоенное произведение этих сторон на косинус угла меду ними. В общем виде: а2=в2+с2-2вс соsa) АВ2=49+529-322cos105 (сos105=-cos75 -по формулам приведения)
Подставьте значения и посчитайте
ответ:А) 10сторон
Б)10 сантиметров
Объяснение:26 - 2*5 = 16 (cм) - длина сторон-оснований.
16/2 = 8 (см) - длина средней линии.