В параллелограмме противоположные углы равны по определению.
Так как противоположные стороны параллелограмма параллельны, то сумма его внутренних односторонних углов, как углов при параллельных прямых и секущей, равна 180º.
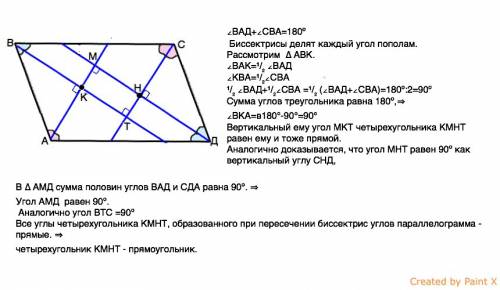
∠ВАД+∠СВА=180º
Биссектрисы параллелограмма делят каждый его угол пополам.
Рассмотрим ∆ АВК.
∠ВАК=¹/₂ ∠ВАД
∠КВА=¹/₂∠СВА
¹/₂ ∠ВАД+¹/₂∠СВА =¹/₂ (∠ВАД+∠СВА)=180º:2=90º
Сумма углов треугольника равна 180º,⇒
∠ВКА=в180°-90°=90°
Вертикальный ему угол МКТ четырехугольника КМНТ равен ему и тоже прямой.
Аналогично доказывается, что угол МНТ равен 90º как вертикальный углу СНД,
В ∆ АМД сумма половин внутренних односторонних углов ВАД и СДА равна 90º. ⇒
Угол АМД равен 90º.
Аналогично угол ВТС =90º
Все углы четырехугольника КМНТ, образованного при пересечении биссектрис углов параллелограмма - прямые. ⇒
четырехугольник КМНТ - прямоугольник.
Там получается 2 прямоугольных треугольника, у который общая сторона - перпендикуляр. По теореме Пифагора находим перпендикуляр. Через 2 прямоугольника, у которых известен катет.
Если разность длин наклонных 5 см, то там, где проекция 7 см - гипотенуза равна х-5, а где проекция 18 см, - х. (чем больше проецкия, тем больше наклонная)
Итак находим перпердикуляр для каждого треугольника и приравниваем...
X^2-324= (x-5)^2-49
Отсюда Х= 30 см. - это мы нашли одну из наклонных.
По теореме пифагора 30^2=324-H^2
H= корень из 576 см