т.к.дан прямоугольник, то по сво-ву диагонали этого прям-ка точкой пересечений будут делиться попалам. рассмотрим треу-к, с углом 80градусов. т.к.две стороны боковые равны, то этот реугольник будет равнобедренным по определению, тогда по теореме о равнобедренном треу-ке углы при основании будут равны, обозначим их по хградусов. по теореме о сумме углов в треу-ке имеем:х+х+80=180, т.е.2х=180, отсюда х=(180-80)/2, х=50
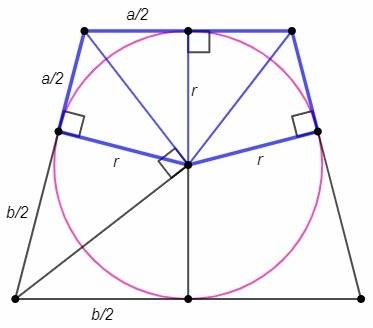
Около трапеции описана окружность, следовательно трапеция равнобедренная (т.к. сумма противолежащих углов равна 180). Биссектрисы углов при основании образуют равнобедренный треугольник (половины равных углов равны). Радиус вписанной окружности делит основание пополам (т.к. является высотой и медианой). Отрезки касательных, проведенных из одной точки, равны. Таким образом, искомый пятиугольник разделен на четыре равных (по двум катетам) прямоугольных треугольника.
S= 4*(a/2)r/2 =ar
Биссектрисы углов при боковой стороне перпендикулярны (т.к. сумма односторонних углов при параллельных равна 180). Радиус к боковой стороне является высотой из прямого угла и равен среднему пропорциональному проекций катетов.
r= √(a/2*b/2) =√(ab)/2
S= a√(ab)/2 =3√15/2
ABCD - прямоугольник. О - точка пересечения диагоналей. АВ - меньшая сторона.
По условию: угол АОВ = 80 гр
Тр-к АОВ - равнобедренный, так как диагонали в прям-ке - равны.
Значит угол ОАВ = (180 - 80)/2 = 50 - искомый угол между диагональю и меньшей стороной.
ответ: 50 град.