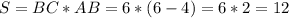 см²
см²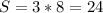
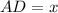 . Тогда
. Тогда 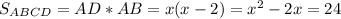
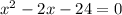 . По теореме Виета находим его корни:
. По теореме Виета находим его корни: 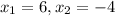 . Так как длина не может быть отрицательной, то выбираем первый корень.
. Так как длина не может быть отрицательной, то выбираем первый корень. 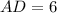 .
. 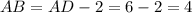 см
см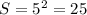 .
.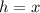 . Тогда наша сторона будет равна
. Тогда наша сторона будет равна  . Учитывая, что площадь треугольника равна
. Учитывая, что площадь треугольника равна 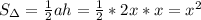 , приравняем это к площади квадрата.
, приравняем это к площади квадрата.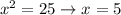
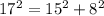 , что делает наш треугольник прямоугольным. Две высоты будут равны соответственно катетам, а третью мы найдем через площадь. Вот как:
, что делает наш треугольник прямоугольным. Две высоты будут равны соответственно катетам, а третью мы найдем через площадь. Вот как: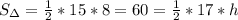
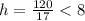 . ответ:
. ответ: 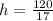
У нас дана правильная четырёхугольная пирамида, следовательно в основании лежит квадрат. Площадь квадрата 64 следовательно его сторона=8, а периметр=32(Это я думаю понятно почему).
Сечение проходящее через вершину S и диагональ основания пирамиды является равнобедренным треугольником его площадь вычисляется по формуле S=1/2*b*h где b основание этого треугольника, а h его высота , выражаем h =2S/b
Основание b является диагональю квадрата лежащего в основании пирамиды и вычисляется по формуле b = √2*a где a сторона квадрата равная 8, соответственно b=√2*8 Тогда h =2*64/√2*8=√128
Апофему вычисляем по теореме Пифагора H=√ h²+a/2² =√144=12 (a/2² потому что это половина стороны квадрата лежащего в основании пирамиды то есть 4)
S боковое=1/2*32*12=192
ответ: 192