ответ: задание 1 практическое, возьмите циркуль и на линейке расположите ножки циркуля так, чтобы расстояние между ними составляло 1,5см и начертите окружность.
Объяснение: задание 2
В прямоугольном треугольнике сумма острых углов составляет 90°. Пусть один из углов будет х, тогда второй угол будет х+20. Составим уравнение:
х+х+20=90
2х=90-20
2х=70
х=70÷2
х=35; 1-й угол =35°, тогда 2-й угол будет 35+20=65°; 2-й угол =65°
Задание 3
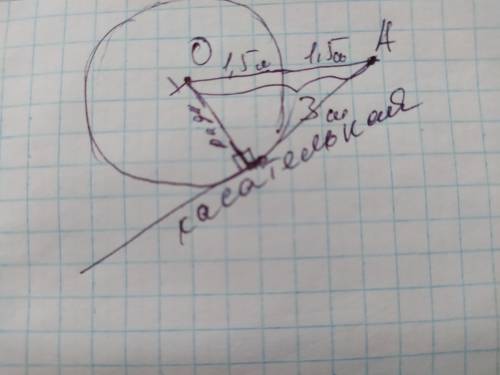
Радиус окружности, проведённый к касательной образует с ней прямой угол 90°, поэтому угол ОРМ=90°. Зная что угол КРМ=25°, найдём угол РОК:
Угол РОК=90-25=65°; угол РОК=65°
ЗАДАНИЕ 4
Рассмотрим ∆АСО и ВДО. У них:
1) СД и АВ пересекаются и при пересечении образуют углы АОС и ВОД, которые равны между собой
2 СД и АВ - диаметры 2-разных окружностей, которые пересекаются в её центре, значит, пересекаясь в точке О, они делятся в равных частях, которые соответствуют их радиусам. Поэтому СО=ДО, АО= ОВ.
Эти треугольники равны по двум сторонам и углу между ними
геометрия (9 класс)
Найти длину окружности ,описанной около равнобедренного треугольника с основанием 10 см и углом 30° при основании .
Дано: ∠A = ∠C =30 ° , AC=b =10 см
----------------------------
R - ?
решение : Можно разными но геометрия (9 класс)
→ рационально использовать теорема синусов :
a/sin∠A = b /sin∠B = c /sin∠C = 2R
Угол против основания ∠B =180° - (30°+30°) = 180° - 60° 120°
AC/sin∠B =2R ⇔ R = AC/2sin∠B
R = 10 /2sin(180° - 60°) =10/2sin60° =10/ (2*√3 / 2) =10 /√3 =( 10√3) /3