35114225 35113996
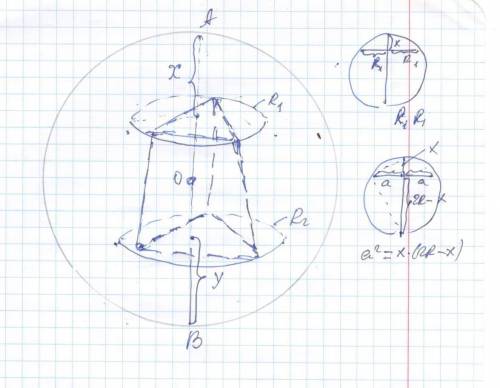
Высота усеченной правильной пирамиды равна 7 см, а длины сторон оснований 3√3 см и 4√3 см. Вычислить радиус описанного шара
R₁ =3√3* √3 /3 = 3 * * * R =(a√3/2)*2/3 =(a√3)/3 * * *
R₂ =4√3* √3 /3 = 4
R₁² = x (2R - x) ⇔x² - 2Rx + 9 = 0 ⇒ x₁ =R -√(R²- 9)
Маленький кусок диаметра x₁ =12 (между основания со стороной 3√3 и поверхностью шара) ( большой кусок x₂=R+√(R²- 9) )
Аналогично
R₂² = y (2R -y) ⇔ y² - 2Ry + 16=0 ⇒ y ₁ = R -√(R²- 16 )
x₁+ H + y₁ = 2R ⇔ R -√(R²- 9) + 7 + R -√(R²- 16) = 2R ⇔
R -√(R²- 9) + 7 + R -√(R²- 16) =2R ;
√(R²- 9) + √(R²- 16) =7 * * * ясно R =5 * * *
примитивное иррациональное уравнение ,необяз. замена t =R² > 0
√(t- 16) = 7 - √(t - 9) ⇔ t- 16 =49 -14√(t - 9) + t -9⇔ 14√(t - 9) =56 ⇔
t - 9 = 4² ⇔ t =25 * * * 3 ; 4 ;5 * * *
R² =25 ⇒ R = 5 ( R = -5 построенное решение )
ответ : 5 см .
Пусть тропеция будет АВСD ,Где AD-большее основание ВС-меньшее основание ,уголАВС-тупой, ВД - его биссектриса, углы АВД=ДВС=у угол ВАД=180-2у (углы ВАД и АВС - односторонние при секущей АВ).
Тогда в треугольнике АВД угол А равен 180-2у, АВД - у, а значит угол ВДА - тоже у (по сумме углов треугольника), и треугольник АВД - равнобедренный. Тогда АВ=АД Пусть АВ=АД=СД=х, тогда по условию 3х +3= 42 , х =13
Так как около любой равнобокой трапеции можно описать окружность, то ее площадь можно рассчитать по формуле Герона.
Полупериметр р=21,S=SQR((21-8)^3 *(21-3))=96. sqr() - корень квадратный.