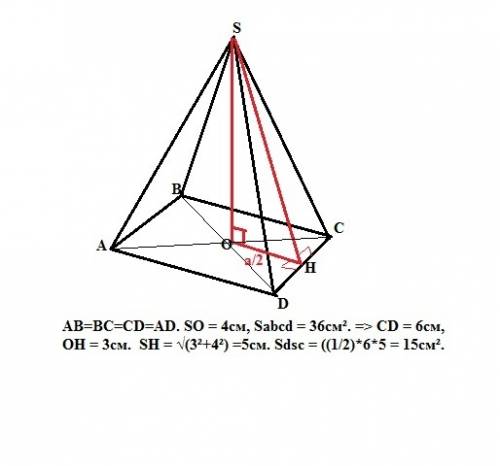
Объем пирамиды: V=(1/3)*So*H, где So - площадь основания пирамиды, H - высота пирамиды. Объем и высота нам даны, найдем площадь основания. So = 48*3/4 = 36 ед². Пирамида правильная, значит в основании лежит квадрат со стороной а = √36 = 6ед, а вершина пирамиды проецируется в центр основания - точку пересечения его диагоналей. Боковые грани нашей пирамиды - равные равнобедренные треугольники. Найдем высоту грани (апофему) из прямоугольного треугольника, образованного высотой пирамиды, половиной стороны основания (катеты) и апофемой (гипотенуза). Ап = √(3²+4²) =5ед.
Тогда площадь одной боковой грани равна Sгр=(1/2)*а*Ап или Sгр=(1/2)*6*5 = 15ед², а площадь боковой поверхности равна
Sбок = 4*Sгр. = 60 ед².
ответ: Sбок = 60 ед².
Доказательства в объяснении.
Объяснение:
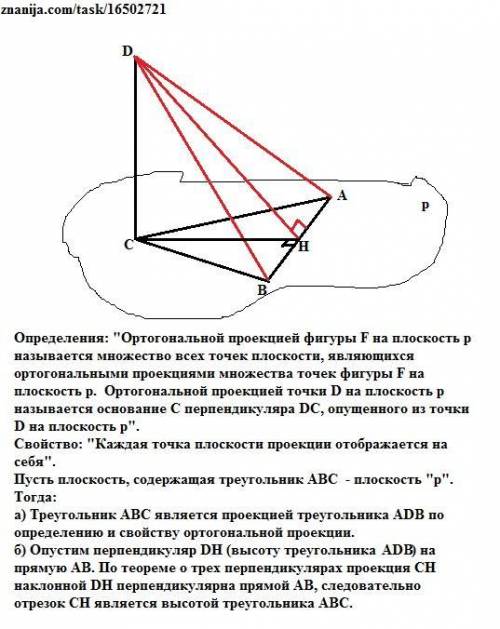
Определения: "Ортогональной проекцией фигуры F на плоскость p называется множество всех точек плоскости, являющихся ортогональными проекциями множества точек фигуры F на плоскость p. Ортогональной проекцией точки D на плоскость p называется основание C перпендикуляра DC, опущенного из точки D на плоскость p".
Свойство: "Каждая точка плоскости проекции отображается на себя".
Пусть плоскость, содержащая треугольник АВС - плоскость "р".
Тогда:
a) Треугольник АВС является проекцией треугольника ADB на плоскость "р" по определению и свойству ортогональной проекции, так как точка С является проекцией точки D на плоскость р, а точки А и В лежат в плоскости р, то есть отображаются сами на себя.
б) Опустим перпендикуляр СH (высоту треугольника АВC) на прямую АВ. По теореме о трех перпендикулярах наклонная DH перпендикулярна прямой АВ, так как проекция СН этой наклонной перпендикулярна прямой АВ. Следовательно, наклонная DН является высотой треугольника АВD. Что и требовалось доказать.
Напомним tgx = 1/ctg x или tg x * ctg x = 1
а) 2 sin 60°•ctg 60° = 2 * √3/2 * √3/3 = (3*2)/(3*2) = 1
в) 7 tg30°•ctg 30° = 7 * √3/3 * √3 = 7
б) 2 sin 45° - 4 cos 30° = 2 * √2/2 - 4 * √3/2=√2- 2√3
г) 6 ctg 60°- 2 sin 60° = 6 * √3/3 - 2 * √3/2 = 2√3 - √3