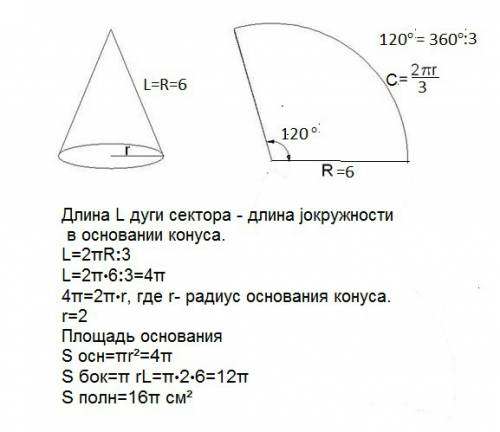
Развёрткой боковой поверхности конуса является круговой сектор радиуса 6 см и дугой 120 градусов. Найдите площадь поверхности конуса.
-------------------------
Если данный сектор свернуть так, чтобы концы дуги сошлись, а боковые стороны – радиусы окружности, частью которой является этот сектор, – совместились, получим наш конус. При этом радиус кругового сектора будет его образующей, а длина дуги - длиной окружности в основании конуса.
Площадь поверхности конуса - сумма площадей основания и боковой поверхности.
Данная развертка - третья часть круга, т.к. ее градусная мера - треть от полной окружности. Площадь сектора = площади боковой поверхности конуса.
Длина С дуги сектора - длина окружности основания конуса.
С=2πR:3
С=2π•6:3=4π
4π=2π•r, где r- радиус основания конуса.
r=2
Площадь основания
S осн=πr²=4π см²
S бок=π r L=π•2•6=12π или πR²:3=(36π:3=12) см²
S полн=16π см²
13. От точки A опускаешь высоту до прямой а, так как расстояние это есть длина перпендикуляра. Получится прямоугольный треугольник, опущенная высота лежит против угла 30° и является катетом, значит этот катет равен половине гипотенузы, а гипотенуза равна 4 см, следовательно расстояние от A до a = 2 см
14. Треугольник равнобедренный, так как углы при основании равны. Также опускаешь высоту до прямой а, эта высота будет являться также медианой так как треугольник равнобедренный, значит высота будет равна 14/2 см = 7см. Так как образованный треугольник также будет равнобедренным, потому что - углы по 45° и 90° . Надеюсь разберешься)
В равнобедренном треугольнике есть свойство что высотоа, бессектриса и медиана совпадают следовательно угол ECD=105