Утверждение В) верно, но только для прямых, лежащих в одной плоскости.
Объяснение:
Определение: "Две прямые, пересекающиеся под прямым углом, называются перпендикулярными" (для плоскости).
Определение: "Две прямые называются перпендикулярными, если угол между ними равен 90°". (для пространства). При этом они не имеют общей точки.
Утверждение А) не верно, так как отрезок по определению - часть прямой, ограниченная двумя точками. Отрезки, лежащие на перпендикулярных прямых, могут располагаться на участках этих прямых, не включающих точку пересечения.
Утверждение Б) не верно по этой же причине, так как луч - это часть прямой, имеющий начальную точку и его можно продолжить только в одну сторону. Лучи, лежащие на перпендикулярных прямых, могут располагаться на участках этих прямых, не включающих точку пересечения.
Утверждение В) верно, если прямые лежат в одной плоскости.
Утверждение Г) не верно по причине, указанной для утверждений А и Б.
1. ΔABC-правильный . R и r-радиусы вписанной и описанной окружностей. Выразите R через r.
a₃ = 2r√3 и a₃ = R√3 ⇒ 2r√3= R√3 , R=2r.
4. Найдите площадь равностороннего треугольника, вокруг которого описано окружность радиуса 3 см.
a₃ = R√3 ⇒ a₃ = 3√3 см
S(равностороннего треуг.)=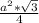
⇒ S(равн.треуг.)= 
= 
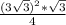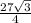(cм²)
5. Определите количество сторон правильного многоугольника углы которого равны 160 градусов.
Многоугольник правильный , поэтому сумма всех внутренних углов 160*n .
160*n=180(n-2) , 160n=180n-360 , 20n=360 , n=18. Количество сторон 18.
((n-2)/n*180- формула для нахождения углов в правильном многоугольнике )
6. В правильный треугольник ,сторона которого 4√3 cм, вписана окружность. Вокруг окружности описан квадрат. Найдите сторону квадрата.
a₃ = 2r√3 , 4√3= 2r√3 ⇒ r=2 см.
Квадрат описан около окружности, значит сторона квадрата равна
a₄ =2r или a₄ =4см.