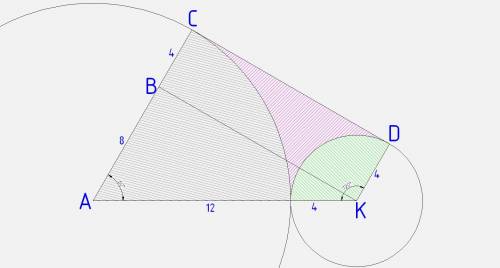
АСДК - трапеция, основания АС=12 см и ДК=4 см
АВ = 12-4 = 8 см
АК = 12+4 = 16 см
По Пифагору
ВК² = АК²-АВ² = 16²-8² = 256-64 = 3*64
ВК = 8√3 см
∠ВАК = arccos(АВ/АК) = arccos(1/2) = 60°
∠ВКА = 90 - ∠ВАК = 30°
∠ДКА = ∠ВКА + 90 = 120°
Полная площадь трапеции
S(ACDK) = 1/2(AC+DK)*BK = 1/2(12+4)*8√3 = 64√3 см²
Площадь сектора большого круга (серая штриховка)
S₁₂ = πR²/360*α = π*12²*60/360 = π*12*12/6 = 24π см²
Площадь сектора малого круга (зелёная штриховка)
S₄ = πR²/360*α = π*4²*120/360 = π*16/3 = 16π/3 см²
И площадь странной фигуры около касательной
S = S(ACDK) - S₁₂ - S₄ = 64√3 - 24π - 16π/3 см²
S = 64√3 - 88π/3 см²

5 cm²
Объяснение:
Добудуємо трикутник так щоб ∠N та ∠M були прямими і обчислимо його площу як різницю площі прямокутника BNCM та ΔBNC та ΔAMB
S ABC = S BNCM - S ΔBNC - S ΔAMB
S ΔBNC = 1/2 S BNCM
S ABC = 1/2 * S BNCM - S ΔAMB
∠BAM = 180° - 150° = 30°
Розглянемо ΔAMB . це прямокутний трикутник, в якого є кут 30° та відома гіпотенуза. Обчислимо катети ΔAMB.
МB = 1/2 AB = 1/2 *4 = 2
AM = 4²-2² =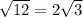
S ΔAMB = 1/2 * AM * MB = 1/2 * 2 *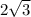 =
= 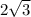
Відрізок MC = CA + AM = 5 +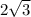
S BNCM = MB * MC = 2 * (5+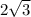 )
)
S ABC = 1/2 * 2 * (5+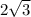 ) -
) - 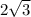 = (5+
= (5+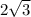 ) -
) - 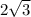 = 5
= 5