1) АС - диагональ и делит параллелограмм на два равных треугольника. Можно вычислить площадь треугольника АВС по ф.Герона. А можно вспомнить. что треугольник со сторонами 5,12, 13 - из Пифагоровых троек, которая, наряду с треугольниками, имеющими отношение сторон 3:4:5 встречается в задачах наиболее часто. Пифагорова тройка— комбинация из трёх целых чисел , удовлетворяющих соотношению Пифагора: с²=a²+b² Следовательно, ∆ АВС - прямоугольный, и его площадь равна половине произведения катетов: S ∆ FDC=5•12=60:2=30 Параллелограмм состоит из двух таких треугольников. S (ABCD)=2•30=60 (ед. плодащи) 2) Одна из формул для нахождения площади треугольника: S=a•b•sin α, где а и b - стороны, α - заключенный между ними угол. Синус 45º=√2):2 S=10•2•√2):2=5√2 (ед. площади)
Найдём сторону a правильного многоугольника, вписанного в окружность с радиусом R:
где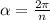 , n — число сторон правильного многоугольника.
, n — число сторон правильного многоугольника.
Для правильного треугольника имеем: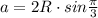 .
.
Найдём сторону A правильного многоугольника, описанного около окружности с радиусом r:
Для частного случая правильного треугольника: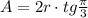
Окружность у нас одна и та же (R = r).
Находим отношение сторон:
Итак, сторона описанного равностороннего треугольника в два раза больше вписанного.
Площадь равностороннего треугольника со стороной a:
где h — высота треугольника,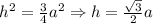 .
.
Следовательно, площади относятся друг к другу как квадраты сторон.
P.S. Решения правятся только со второй-третей попытки.