ответ: Пусть ABC — произвольный треугольник. Проведём через вершину B прямую, параллельную прямой AC. Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC. Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD. Сумма всех трёх углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Что и требовалось доказать.
Объяснение: Из теоремы следует, что у любого треугольника не меньше двух острых углов. Действительно, применяя доказательство от противного, допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть, по крайней мере, два угла, каждый из которых не меньше 90°. Сумма этих углов не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°.
РЕШЕНИЕ
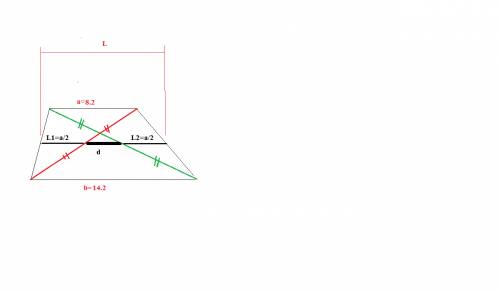
сделаем построение поусловию
основания a=8.2 b=14.2
по теореме Фалеса
прямая, которая делит диагонали пополам -также будет делить пополам боковые стороны
на этой же прямой лежит средняя линия трапеции L=(a+b)/2
на верхнем основаниии можно построить ДВА треугольника
1-ый с вершиной в нижнем левом углу трапеции L1=a/2
2-ой с вершиной в нижнем правом углу трапеции L2=a/2
среднии линии этих треугольников также лежат на средней линии трапеции
тогда расстояние между серединами ее диагоналей
d=L-L1-L2=(a+b)/2 -a/2-a/2=( (a+b) -2a) /2 =(b-a)/2 =(14.2-8.2)/2=6/2=3 см
ОТВЕТ 3 см
Думаю все понятно))))