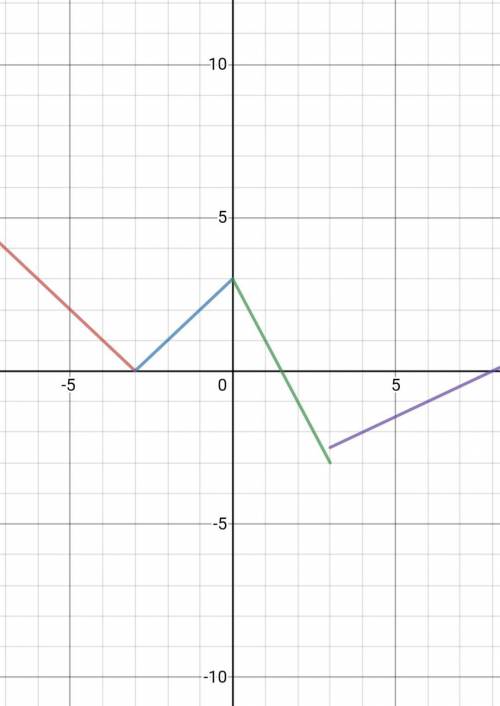
Чтобы построить график такой функции, вам нужно чертить каждую часть отдельно.
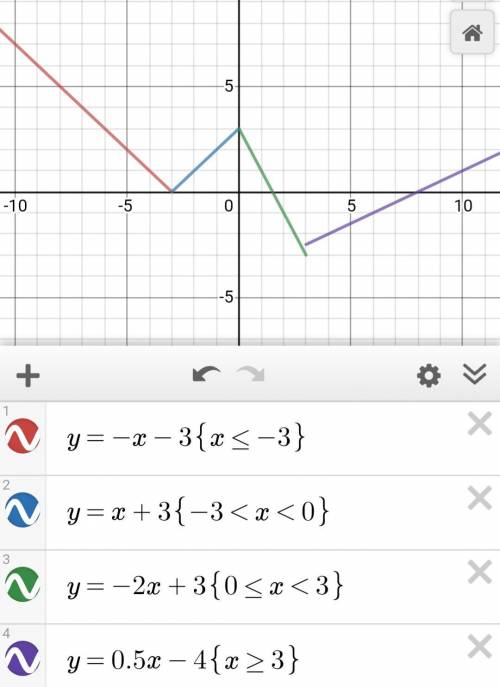
1) f(x)= –x–3 , если х ⩽ –3. Это значит, что если х больше –3, то этой функции уже не существует.
f(x)= –x–3 линейная функция. Чтобы нарисовать ее график, достаточно знать пару ее точек.
f(–3)= –(–3)–3=0 — точка (–3; 0).
f(–5)= –(–5)–3=2 — точка (–5; 2).
Соединяете точки и проводите таким образом луч (который имеет начало в точке (–3; 0) и уходит влево). Это красная линия на графике.
2) f(x)= x+3, если –3 < х < 0.
Достаточно знать координаты пары самых крайних точек.
f(–3)= –3+3= 0 — точка (–3; 0)
f(0)= 0+3= 3 — точка (0; 3).
Очевидно, что данные точки не принадлежат графику, так как –3 < х < 0, однако на графике этого не будет видно и будет казаться, что х=3, хотя на самом деле самая крайняя точка будет иметь абсциссу х=–2,999....99.
(Синяя линия на графике)
Так же само рисуете и остальные две части графика.
3) f(x)= –2x+3, если 0 ⩽ х < 3.
Крайние точки:
f(0)= 3 — точка (0; 3)
f(3)= –6+3= –3 — точка (3; –3)
(Зеленая линия на графике)
4) f(x)= 0,5x–4, если х ⩾ 3.
f(3)= 0,5×3–4= 1,5–4= –2,5 — точка (3; –2,5)
f(4)= 0,5×4–4= 2–4= –2 — точка (4; –2)
(Фиолетовая линия на графике)
а) Доказано; б) 36
Объяснение:
а)
Обратимся к первому рисунку. Пусть ∠AOB=∠COD=ω. Тогда ∠BAO=∠ABO=∠OCD=∠ODC=α (AO=OB=R и CO=OD=R => треугольники ABO и COD равнобедренные, в которых угол против основания общий, а =>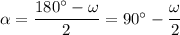
). ΔAOD равнобедренный (AO=OD=R) => ∠OAD=∠ODA=β. Аналогично ∠OBC=∠OCB=γ. Т.к. четырехугольник вписан в окружность, то ∠BAD+∠BCD=180°. Значит: 
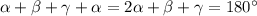. ∠BAD+∠ABC=
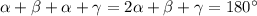. Получили, что 
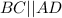, т.к. внутренние односторонние углы при этих прямых и секущей AB в сумме дают 180°. Поскольку AD≠BC (по условию AD=2BC), четырехугольник трапеция, а не параллелограмм, а так как она вписана в окружность, то равнобедренная. Доказано.
Заметим, что центр описанной около четырехугольника окружности может лежать вне него. Тогда доказательство будет отличаться. Начиная с этого момента забудем о тех обозначениях, которые были введены для доказательства первого случая. Обратимся ко второму рисунку. Заметим, что ∠ABC=∠BCD=α, так как AO=OB=R и CO=OD=R => треугольники ABO и COD равнобедренные, в которых угол против основания общий, а =>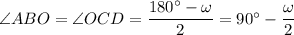
(здесь ∠AOB=∠COD=ω) и ∠OBC=∠BCO, так как это углы при основании равнобедренного треугольника BOC (OB=OC=R). Пусть ∠BAD=β. Тогда 
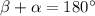(так как четырехугольник вписанный). Но 
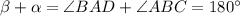. Значит 
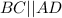, т.к. внутренние односторонние углы при этих прямых и секущей AB в сумме дают 180°. Поскольку AD≠BC (по условию AD=2BC), четырехугольник трапеция, а не параллелограмм, а так как она вписана в окружность, то равнобедренная. Доказано.
б)
Решим задачу для 1-ого случая:
Пусть EG - расстояние между прямыми BC и AD. Т.к. BC||AD, то EG=6. Заметим, что треугольники BOC и AOD равновеликие.
Докажем это:
Пусть ∠BOC=α. Тогда (так как ∠AOB=∠COD=90°, а => ∠BOC+∠AOD=360°-90°-90°=180°) ∠AOD=180°-α.
Получим:
Запишем их площади через формулу про основание и высоту:
Из условия следует, что AD=2BC.
Тогда:
Знаем, что:
Тогда:
Поскольку треугольники BOC и AOD равнобедренные, то OG и OE не только их высоты, но и медианы соответственно, а значит BG=BC/2 и AE=AD/2.
Тогда из прямоугольных треугольников BOG и AOE по теореме Пифагора найдем BC и AD:
По условию AD=2BC.
Значит:
Теперь находим BC и AD:
Теперь можно без труда найти площадь трапеции:
Получили, что площадь трапеции ABCD равна 36.
Задача решена!
(Для второго случая решить пункт б) невозможно, так как дуга AB + дуга CD по условию должны давать 180°, что невозможно для данного случая)