Дан четырехугольник ABCD
AB=CD
BC=AD
угол A = 30⁰
E ∋ BC
угол CDE = 60⁰
Доказать. ABED - прямоугольная трапеция.
Доказательство.
Рассм. ABCD. угол A = 30⁰ ⇒ угол С = 30⁰
угол В = углу D = (360⁰ - 30⁰ - 30⁰)/2 = 300⁰/2 = 150⁰
угол ADE = угол ADC - угол CDE
т.к. угол ADC 150⁰, a по условию угол CDE = 60⁰, то угол AED = 150⁰ - 60⁰ = 90⁰
Опеределения:
- трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны.
- трапеция, один из углов которой прямой, называется прямоугольной
Рассмотрим ABED - четырехугольник.
BE||AD,
AB не параллельно ED (т.к. ED перпендикуляр к AD)
угол EDA - 90⁰
След-но ABED - прямоугольная трапеция.
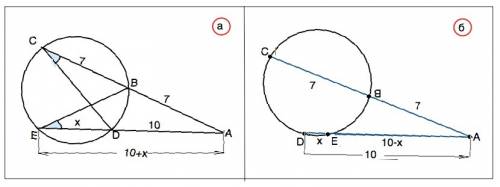
Теорема: Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. По данным условия логично предположить, что если на одной секущей точки идут в порядке А, В, С, то на другой - А, D, E. ( Заметим, что свойство секущих легко доказывается из подобия ∆ ADC и ∆ ABE - угол А общий, вписанные углы Е и С равны, как опирающиеся на одну дугу). Следовательно, АС•АВ=АЕ•AD
Тогда АС=14, АЕ=10+DE. Примем DE=х. ⇒ 98=(10+х)•10, но решение этого уравнения даёт отрицательное значение DE.
Следовательно, условие не совсем верное, и возможны варианты, например:
а) АВ=7, ВС=17. Тогда АС=24, АЕ=10+х,⇒ 24•7= 10•(10+х), откуда получим DE=6,8.
б) Более вероятный. Все численные значения задачи верны, но у второй секущей АD=10, DE=x, внешняя часть секущей - АЕ= 10-х. Составим и решим уравнение: 14•7=10•(10-х). 98=100-10х ⇒ DE=х=0,2 ед. длины.
Решение на фото