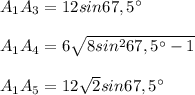
Объяснение:
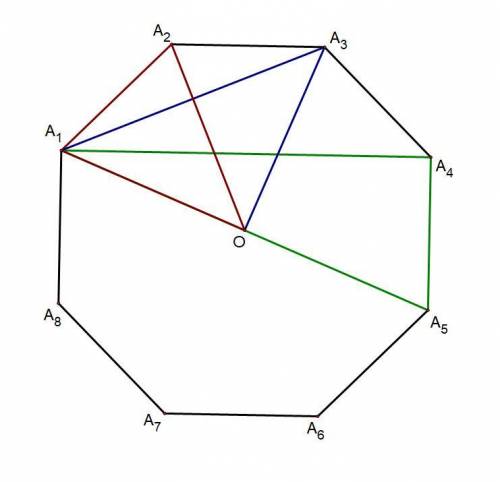
Пусть O -- центр правильного многоугольника.
Если из точки O провести отрезки OA₁, OA₂,..., ОA₈, то получится 8 равных равнобедренных треугольников (по трём сторонам). Углы при вершинах этих треугольников будут равны и в сумме давать 360°. Тогда:
1. 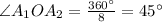
Рассмотрим ΔOA₁A₂:
A₁A₂ = 6, ∠O = 45°
∠A₁ = ∠A₂ (свойство р/б Δ)
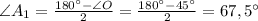
Применим теорему синусов:
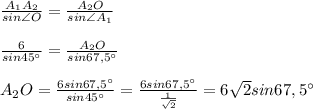
2. A₁A₅ = 2A₁O = 2 * 6√2 sin67,5° = 12√2 sin67,5°
3. Рассмотрим ΔA₁A₃O:
∠A₁OA₃ = 2∠A₁OA₂ = 90°
A₁O = OA₃ = 6√2 sin67,5°
В р/б прямоугольном треугольнике гипотенуза равна катету, умноженному на √2, т.е.
A₁A₃ = √2 * 6√2 sin67,5° = 12 sin67,5°
4. Рассмотрим ΔA₁A₄A₅:
A₁A₅ = 12√2 sin67,5°, A₄A₅=6
∠A₁A₄A₅ = 90°
По теореме Пифагора найдём гипотенузу A₁A₄:
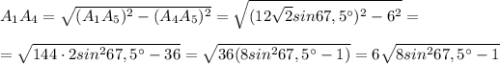
Высота правильной четырёхугольной пирамиды равна 12 см, а сторона основания равна 24 см. Вычисли двугранный угол при основании.
——————————————————
Основание правильной четырехугольной пирамиды – квадрат.
Все боковые грани правильной пирамиды образуют с плоскостью основания равные углы, а высота проходит через центр основания, который является центром вписанной и описанной около основания окружностей.
Двугранный угол здесь образован радиусом вписанной окружности и апофемой, как отрезками. перпендикулярными ребру основания в одной точке (по т. о трех перпендикулярах).
Радиус вписанной в квадрат окружности равен половине его стороны.
r=24:2=12 (см)
Соединив основание апофемы с центром основания ( основанием высоты пирамиды), получим прямоугольный треугольник.
При этом катеты- высота пирамиды и половина стороны основания - равны 12 см.
Следовательно, треугольник - равнобедренный. Острые углы равнобедренного прямоугольного треугольника равны 45º.⇒ Искомый угол равен 45º.