∠АВН = 30°; ∠ВАР = 45°.
Пошаговое объяснение:
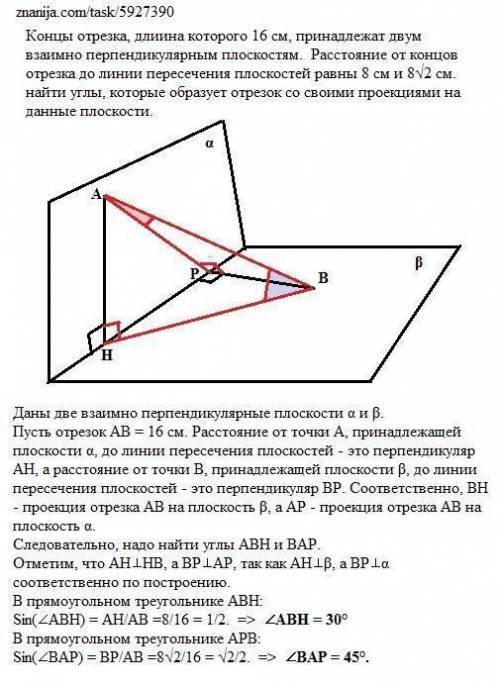
Концы отрезка, длина которого 16 см, принадлежат двум взаимно перпендикулярным плоскостям. Расстояние от концов отрезка до линии пересечения плоскостей равны 8 см и 8√2 см. найти углы, которые образует отрезок со своими проекциями на данные плоскости.
Решение.
Даны две взаимно перпендикулярные плоскости α и β.
Пусть отрезок АВ = 16 см. Расстояние от точки А, принадлежащей плоскости α, до линии пересечения плоскостей - это перпендикуляр АН, а расстояние от точки В, принадлежащей плоскости β, до линии пересечения плоскостей - это перпендикуляр ВР. Соответственно, ВН - проекция отрезка АВ на плоскость β, а АР - проекция отрезка АВ на плоскость α.
Следовательно, надо найти углы АВН и ВАР.
Отметим, что АН⊥НВ, а ВР⊥АР, так как АН⊥β, а ВР⊥α соответственно по построению.
В прямоугольном треугольнике АВН:
Sin(∠АВН) = АН/АВ =8/16 = 1/2. => ∠АВН = 30°
В прямоугольном треугольнике АРВ:
Sin(∠ВАР) = ВР/АВ =8√2/16 = √2/2. => ∠ВАР = 45°.
Сначала строится прямоугольный треугольник, у которого катет равен стороне, а гипотенуза - диагонали. Строится он так. На плоскости берутся две взаимно перпендикулярные прямые, от точки их пересечения (это первая вершина прямоугольника, её местоположение выбирается произвольно) вдоль одной их прямых откладывается отрезок, равный стороне прямоугольника, в конечную точку этого отрезка (это вторая вершина прямоугольника) ставится циркуль и проводится окружность радиусом, равным диагонали. Где-то окружность пересечет вторую прямую. Эта точка (это третья вершина прямоугольника) соединяется с центром окружности (со второй вершиной).
Получился прямоугольный треугольник с нужными размерами.
Теперь надо достроить его до прямоугольника, для этого надо через концы гипотенузы провести прямые параллельно противоположным катетам. Построить параллельную через заданную точку циркулем и линейкой - это стандартное построение.
Это все.