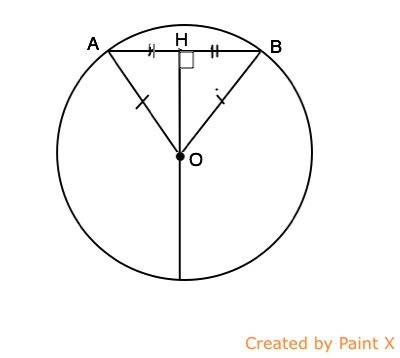
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
Находим расстояние L точки М от начала координат.
L = √(3² + (-6)² + 9²) = √(9 + 36 + 81) = √126 = 3√14.
Пусть искомая точка К равно удалена от точек М и О (начало координат).
Точки М, К и О образуют равнобедренный треугольник.
МО = L = 3√14. MK = KO = d.
Находим косинус угла КОМ:
cos KOM = 9/L = 9/(3√14) = 3/√14.
По теореме косинусов:
cos KOM = 3/√14 = (L² + d² - d²)/(2*L*d) = 126/(2*3√14*d).
Отсюда находим: 2*3*3*d = 126. откуда d = 126/18 = 7.
ответ: точка К (0; 0; 7).