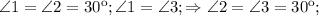 )
) 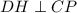 ,
, 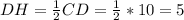 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD. 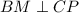 ,
, 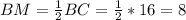 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 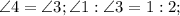
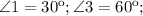 Тогда в ромбе
Тогда в ромбе 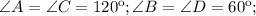
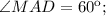 , тогда
, тогда 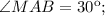 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 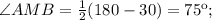
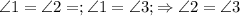 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 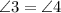 ,
, 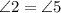 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.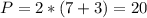 .
.
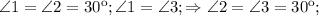 )
) 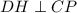 ,
, 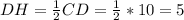 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD. 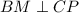 ,
, 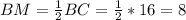 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 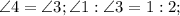
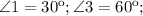 Тогда в ромбе
Тогда в ромбе 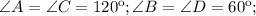
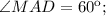 , тогда
, тогда 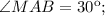 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 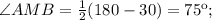
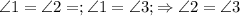 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 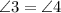 ,
, 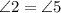 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.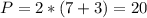 .
.
1. Диаметр = 2*Радиус = 2* 2.5 см = 5 см
Диаметр - это максимально возможная хорда, проходящая через центр,
значит, если диаметр=5см, то хорда не может быть равна 6 см (выходит за пределы окружности)
2. Две окружности касаются, если расстояние между их центрами равно сумме их радиусов.
Если сумма радиусов меньше - то не пересекаются
Если сумма радиусов больше - то они пересекаются, а не касаются!
Р1+Р2 = 25+50 = 75 см,что больше расстояния между центрами окружностей
Значит окружности пересекаются, а не КАСАЮТСЯ!
Удачи!