ответ: S ☐ABCD = 400 см².
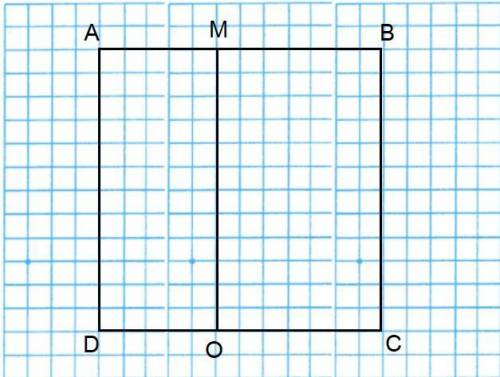
Объяснение: Обозначим квадрат буквами ABCD.
Пусть прямоугольник, периметр которого равен 50 см - DAMO, а прямоугольник, периметр которого равен 70 см - OMBC.
P ▯OMBC = (BC + CO) * 2 = 70 см.
(BC и CO - смежные стороны прямоугольника).
⇒ BC + CO = P/2 ⇒ BC + CO = 70/2 = 35 см.
P ▯DAMO = (AD + DO) * 2 = 50 см.
(AD и DO- смежные стороны прямоугольника).
⇒ AD + DO = P/2 ⇒ AD + DO = 50/2 = 25 см.
AD, DC и CB - стороны данного квадрата.
⇒ AD + DC + CB = 35 + 25 = 60 см.
Т.к. стороны квадрата равны ⇒ AD = DC = CB = 60/3 = 20 см.
⇒ AB = CB = DC = AD = 20 см (т.к. все стороны в квадрате равны).
S ☐ABCD = a² (a - сторона квадрата) ⇒ S ☐ABCD = 20² = 400 см².
Объяснение:
1. Выполняем построение треугольника АВС.
2. Строим график прямой х = -12 . Это вертикальная прямая проходящая через точку (-12; 0)
3. Выполняем построение симметричной фигуры:
от т. А проводим перпендикуляр к прямой х = -12. Откладываем перпендикуляр такой же длины в противоположною сторону от х = -12.
То же самое выполняем для т. В. Т. С совпадает с точкой С1, т.к. абсцисса т. С = -12 и лежит на прямой х = -12.
Координаты ΔA1B1C1 можно определить графически:
А1(-36;4) , В1(-28; -12) , С1(-12; -4).
Также абсциссы можем определить математически:
х1 = -12 - (12+х) = -24-х.
Здесь -12 - это сдвиг координат влево на 12 единиц, (12+х) расстояние между осью симметрии и точками исходного треугольника.
Ординаты остаются неизменными, т.к. ось симметрии - вертикальная.