Во всех задачах (10 , 11 , 12 и 13) ∠C =90° как вписанный угол, опирающийся на диаметр окружности
2.4. 10.
R = 3 ; AB =2R , AC =4√2 .
BC -? 2
Из ΔABC по теореме Пифагора :
BC =√(AB - AC²) =√( (2R)² - AC²) =√(6²-(4√2)²) =√(36-16*2)=√4 =2 .
2.4.11.
AC=11 ; BC =60 ; ∠C=90° (AВ =2R )
R - ? 30,5
см решения предыдущей задачи
AB =√(AC² +BC²) =√(11² +60²)=√(121 +3600) =√3721 =61 ;
R =AB /2 =61/2 =30,5 .
2.4.12.
AC=18 ; BC =4 ; ∠C=90° (AВ =2R )
R - ? 15
AB =√(18² +24²) =√( (6*3)² +(6*4)²)=√6²(3²+4²) =√(6²*5²)=6*5 =30 ;
R =AB/2 =30/2 =15 .
2.4.13.
AC=35 ; ∠COB=120° ; ∠C=90° (AВ =2R )
AB - ?
∠AOC =180° -∠COB=180° - 120° = 60° ; ΔAOC равнобедренный (OA =OC =R) , следовательно и равносторонний OA = OC =AC =35 .
∠OAC =∠OCA = (180° - ∠AOC) :2 =(180° - 60°) :2 =60° .
AB=2*R =2*35 =70 .
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Доказательство.Обратимся к рисунку, на котором АВС — равнобедренный треугольник с основанием ВС, АD — его биссектриса.Из равенства треугольников АВD и АСD (по 2 признаку равенства треугольников:AD-общая;углы 1 и 2 равны т.к. AD-биссектриса;AB=AC,т.к. треугольник равнобедренный) следует, что ВD = DC и 3 = 4. Равенство ВD = DC означает, что точка D — середина стороны ВС и поэтому АD — медиана треугольника АВС. Так как углы 3 и 4 смежные и равны друг другу, то они прямые. Следовательно, отрезок АО является также высотой треугольника АВС. Теорема доказана. В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой Если в треугольнике два угла равны, то он равнобедренный. Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
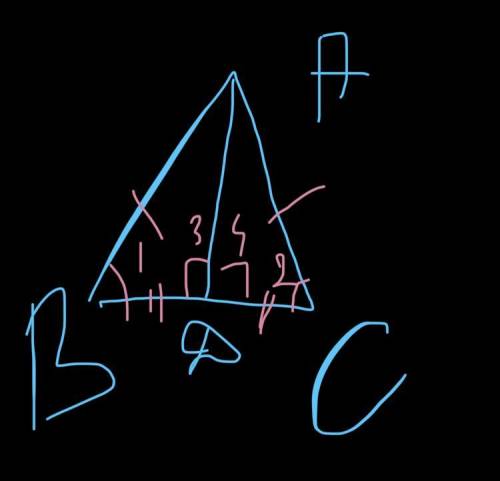
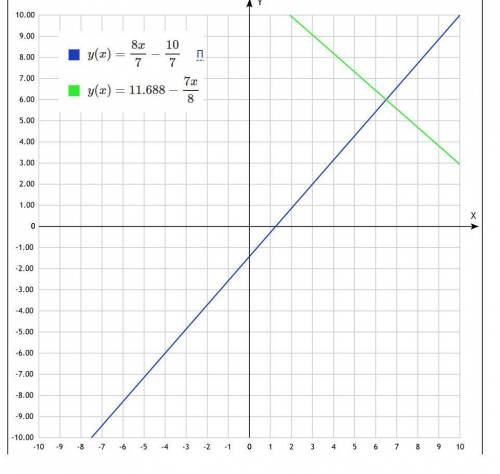
1) уравнение АВ
y=ax+b
подставлю точки
2=3a+b
10=10a+b
система это
из первого b=2-3a и во второе
10=10a+2-3a; 8=7a; a=8/7
подставлю в первое a и найду b
2=3*8/7+b; b=2-24/7=(14-24)/7=-10/7
тогда уравнение прямой AB
y=8x/7-10/7
7y=8x-10
8x-7y-10=0
2) уравнение перпендикулярной линии к АВ имеет вид
7x+8y+c=0 (8*7-7*8=0-скалярное произведение нормалей равно 0 у перпендикулярных прямых)
чтобы вычислить с-надо подставить в него координаты середины О отрезка АВ, через которую проходит искомая прямая
O((3+10)/2;(2+10)/2)=(6.5;6)
7*6.5+8*6+c=0
45,5+48+c=0
c=-93.5
7x+8y-93.5=0-уравнение искомой прямой
10. Вписанный угол АСВ опирается на диаметр АВ=3*2=6, значит, угол АСВ прямой. По теореме Пифагора ВС=√(АВ²-АС²)=√(36-32)=√4=2
ответ ВС=2
11. т.к.10. Вписанный угол АСВ опирается на диаметр АВ=2*R, значит, угол АСВ прямой. По теореме Пифагора АВ=√(ВС²+АС²)=√(121+3600)=√3721=61, тогда радиус - половина диаметра АВ=61/2=30.5
ответ радиус окружности равен 30.5
13. Вписанный угол АСВ опирается на диаметр АВ=2*R, значит, угол АСВ прямой. Угол СОВ- внешний угол при вершине О для треугольника АОС, поэтому равен сумме двух внутренних углов А и С, не смежных с ним, значит, каждый из этих углов по 60°, т.к. ОС и ОА равны как радиусы одной окружности, т.е. ΔАОС равнобедренных, но т.к. сумма углов в треугольнике 180°, то и третий угол СОА тоже 60°, ΔАОС - равносторонний, значит, радиус равен тоже 35, тогда диаметр 35*2=70
ответ 70