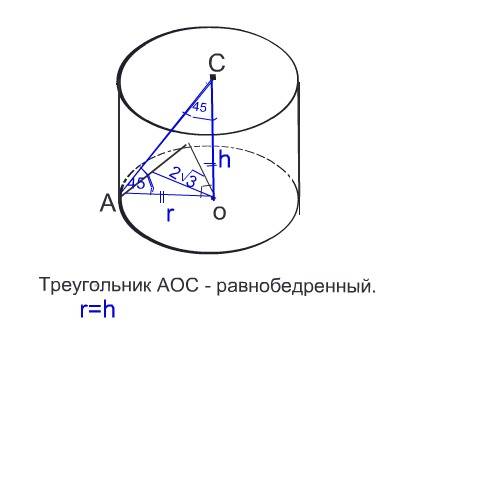
Рисунок во вложении.
Для того, чтобы найти площадь осевого сечения цилиндра нам нужно знать высоту цилиндра и диаметр его оснований.
Так как отрезок, соединяющий центр верхнего основания с одним из концов данной хорды образует с осью цилиндра угол 45 градусов, то этим отрезком, радиусом и осью цилиндра ( высотой его) образуется равнобедренный треугольник. следовательно, высота цилиндра равна радиусу его оснований.
Можем ли вычислить величину этого радиуса? Можем.
Соединим центр окружности с концами хорды и получим равносторонний треугольник, т.к. по условию задачи хорда отсекает от окружности дугу в 60°. Высота этого равностороннего треугольника равна расстоянию от центра основания до хорды и по условию задачи равна 2√3.
Высота равностороннего треугольника равна (а√3):2, где а - сторона этого треугольника.
(а√3):2=2√3см.
Найдем из этого уравнения сторону а( радиус основания).
а√3 =2*2√3
а =4см
Поскольку высота цилиндра равна радиусу оснований, она равна 4см.
Диаметр оснований равен 4*2=8см
Площадь осевого сечения цилиндра D*h равна
4*8=32см²
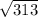
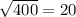
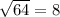
1. Берілген нүктелер арқылы өтетін түзудің теңдеуін жазыңыз: А(2;1) В(-1;2). [2 ұпай]
2. Шеңбердің берілген теңдеуі бойынша оның центрінің координаталары мен радиусын табыңыз: (х-4)2 +(у+8)2 =36 [1 ұпай]
3. нүктелері берілген.
a) төбелерінің координаталары бойынша салыңыз; [1 ұпай]
b) қабырғаларының ұзындықтарын табыңыз; [3 ұпай]
c) түрін анықтаңыз (теңқабырғалы, теңбүйірлі, тікбұрышты); [2 ұпай]
d) берілген үшбұрыштың ауданын есептеңіз. [2 ұпай]
4. Төбелері А (1;-1) В (0;1) С (4;3) және Д (5;1) нүктелері болатын төртбұрыштың тіктөртбұрыш болатынын дәлелдеп, оның ауданын табыңыз. Ол үшін:
a) төбелерінің координаталары бойынша сызбасын салыңыз; [1 ұпай]
b) қабырғаларының ұзындықтарын табыңыз; [4 ұпай]
c) диагональдарын анықтап, дәлелдеңіз; [2 ұпай]
d) тіктөртбұрыштың ауданын есептеңіз. [2 ұпай]
памагит