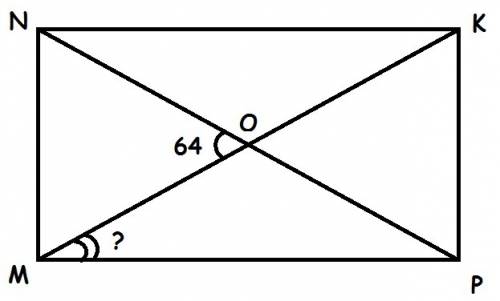
Рассмотрим прямоугольник MNKP
NP = MK т.к. диагонали прямоугольника равны
OM = OK = NO = OP т.к. диагонали параллелограмма в точке пересечения делятся поровну
Рассмотрим треугольник NOM
NO = OM из этого следует, что треугольник NOM равнобедренный, с основанием NM
угол MNO = угол NMO т.к. углы при основании равнобедренного треугольника равны
угол MNO + угол NMO + угол NOM = 180 градусов
= угол MNO + угол NMO + 64 = 180 градусов
180 - 64 = 116
116 : 2 = 58
Угол OMN = 58 градусов
Рассмотрим прямоугольник MNKP
Углы прямоугольника равны 90 градусов
угол OMN + угол OMP = 90 градусов
угол OMN + 58 = 90 градусов
90 - 58 = 32
ответ: Угол OMP равен 32 градусам
Объяснение:
Чтобы найти площадь сечения, которое является кругом, нужно знать его радиус r. Найдем его, рассмотрев сечение шара плоскостью, перпендикулярной искомому сечению (тому, площадь которого мы должны найти). (Смотри рисунок.)
Рассматриваемое сечение - тоже круг, его центр О совпадает с центром шара, а радиус R = 25 см. Проведем хорду АВ. Это - диаметр искомого сечения. Расстояние до него - длина перпендикуляра, опущенного на АВ из точки О (обозначим его ОН). Длина этого перпендикуляра h = 20 см. Получился прямоугольный треугольник ОАН с гипотенузой R и катетами h и r. По теореме Пифагора найдем r:
.
Теперь находим площадь сечения:
≈706,86
КС=6см, АК=8см. ВК+DK= 28см. По свойству пересекающихся хорд: АК*ВK=СК*DК. 8*BK = 6*DK. ВK=(3/4)*DK.