Перша сторона АС=16см
Друга сторона АВ=20см
Третя сторона ВС=24см
Объяснение:
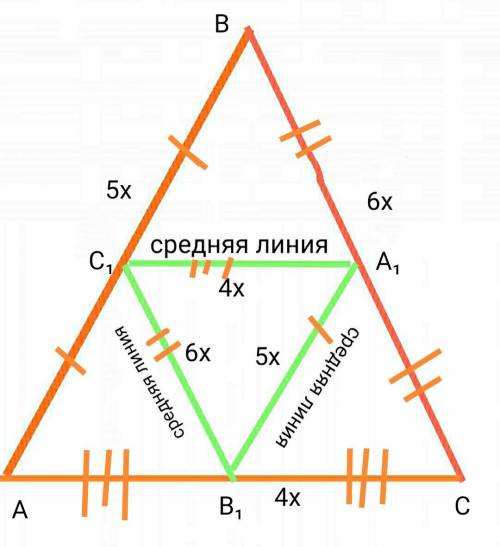
Позначемо вершини трикутника АВС, а вершини трикутника створеного середніми лініями А₁В₁С₁. Вершини ∆А₁В₁С₁ лежать на серединах сторін ∆АВС, тому вони ділять сторони ∆АВС навпіл. А також середня лінія трикутника паралельна протилежній стороні і дорівнює її половині, тому: АС₁=ВС₁=А₁В₁; АВ₁=СВ₁=А₁С₁; ВА₁=А₁С=В₁С₁, тому ∆А₁В₁С₁~∆АВС. Якщо середні лінії ∆А₁В₁С₁ відносяться як 4 : 5 : 6, то сторони ∆АВС будуть мати таке ж саме відношення. Позначемо ці відношення як 4х, 5х та 6х, і якщо відомо, що периметр трикутника 60см, складемо рівняння:
4х+5х+6х=60
15х=60
х=60÷15
х=4
Тоді перша сторона АС=4×4=16см
Друга сторона АВ=5×4=20см
Третя сторона ВС=6×4=24см
Решение, а) По условию Z2 + Z4 = 220°. Эти углы вертикальные, поэтому Z2 = Z4 = 110°.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°, откуда Z1 = 180° -- 110° = 70°.
Углы 3 и 1 вертикальные, поэтому Z3 = Z1 = 70°.
б) Углы 1 и 3, а также 2 и 4 вертикальные, поэтому Z3 = Zl, Z4 = = Z2. Подставив эти выражения в данное равенство, получим:
3(2Z1) = 2Z2,
или
3Z1 =Z2.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°. Из этих двух равенств находим Z1 и Z2: Z1 = 45°, Z2 = 135°.
Z3 = Z1, поэтому Z3 = 45°; Z4 = Z2, поэтому Z4 = 135°
в) По условию Z2 — Z1 = 30°. Эти углы смежные, следовательно, Zl + Z2 = 180°. Из этих двух равенств имеем: Z1 = 75°, Z2 = 105°.
Z3 = Z1, поэтому Z3 = 75°; Z4 = Z2, поэтому Z4 = 105°.
ответ, a) Zl = Z3 = 70°, Z2 = Z4 = 110°; б) Zl =Z3 = 45°, Z2 = = Z4 = 135°; в) Zl = Z3 = 75°, Z2 = Z4 = 105°.