Проанализируем исходные данные.
Дан эллипс с центром в точке (2:-1) и малой осью, равной 4.
Одна из директрис задана уравнением y+5=0, что равносильно у = -5.
Тогда расстояние от центра до директрисы равно |-5 - (-1)| = 4.
Рассмотрим точку эллипса на малой оси. Она удалена от центра на 4 и от директрисы на 4 единицы (так как малая ось параллельна директрисе).
Так как все точки параболы равноудалены от директрисы и фокуса, то получается, что фокус параболы находится в её центре.
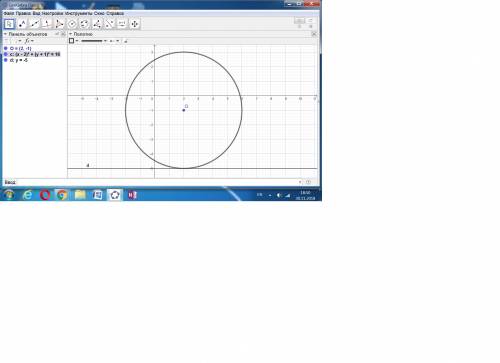
Это говорит о том, что мы имеем не эллипс, а окружность радиуса 4.
Её уравнение: (х - 2)² + (у + 1)² = 4².
Сечением будет равнобедренная трапеция, т.к. основания призмы лежат в параллельных плоскостях, то секущая плоскость их будет пересекать по параллельным прямым.
Пусть К и М середины рёбер АС и ВС, тогда МК средняя линия, по свойству она параллельна третьей стороне АВ и равна её половине - 4 см (стороны основания равны по 8см)
Секущая плоскость проходит через точку А1 и параллельна МК, т.е. совпадает с А1В1 (МК II АВ II А1В1). А1В1МК - трапеция с основаниями А1В1=8см и МК=4см
Боковые стороны равны из равенства прямоугольных треугольников АА1К и ВВ1М (по двум катетам). А1К и В1М - гипотенузы этих треугольников. Их находим по теореме Пифагора √3²+4²=√9+16=√25=5см.
Р=4+8+2·5=22см