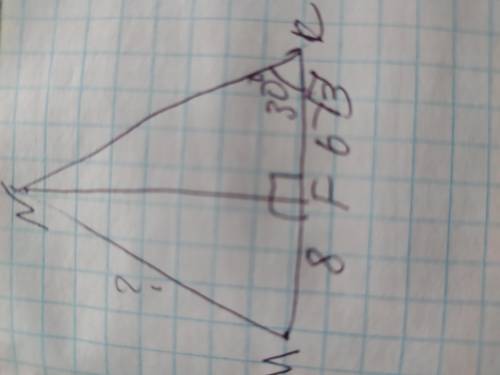
ответ: NM= 10см
Объяснение: высота NF делит ∆ MNK на два прямоугольных треугольника в которых высота NF является катетом. Рассмотрим полученный ∆NKF. По условиям угол NKF составляет 30°, а катет, который лежит напротив этого угла равен половине гипотенузы. Пусть катет NF будет х, тогда гипотенуза NK будет 2х. Составим уравнение и найдём стороны ∆MKF по теореме Пифагора:
NF²+FK²=NK²
x²+(6√3)²=(2x)²
x²+36×3=4x²
x²+108=4x²
x²-4x²= - 108
- 3x²= - 108
3x²=108
x²=108÷3
x²=36
x=6; сторона NF=6см, тогда гипотенуза NK будет 6×2=12см
Теперь найдём искомую сторону NM по теореме Пифагора, зная MF и NF:
NM²=MF²+NF²
NM=8²+6²=√(64+36)=√100=10см
NM=10см
1 вариант: 72°, 72°, 36°
2 вариант:48°, 48°, 84°
Объяснение:
окружность, О- центр, АВ - хорда.
Треугольник АОВ - равнобедренный, т.к. АО=ОВ - радиусы. Значит, ∠А=∠В.
Тогда 2∠А+∠О=180°.
1. Пусть ∠А-∠В=36°, тогда ∠В=∠А-36°
Подставляем в равенство выше, получаем:
3∠А-36=180
∠А=72°, ∠В=72°. Тогда ∠О=180-2∠А=180-144-36°
2. Если ∠В-∠А=36°, тогда ∠В=∠А+36°
Подставляем в равенство выше, получаем
3∠А+36°=180
∠А=48°, ∠В=48°, ТОгда ∠О=180-2∠А=180-96=84°