Дано: А(-3; 9), В(-4; -8), С(6; 0)
Найти:
а)координаты вектора АС;
б)длину вектора ВС;
в)координаты середины отрезка АВ:
г)периметр треугольника АВС;
д)длину медианы СМ.
a) AC = {Cx - Ax ; Cy - Ay}
AC = {6 - (-3) ; 0 - 9}
AC ={9 ; -9}
б) BC = {Cx - Bx ; Cy - By}
BC = {6 - (-4); 0 - (-8)}
BC = {10 ; 8}
|BC| =  =
= 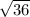 = 6
= 6
в) Пусть это будет точка M, тогда её координаты будут равны
M((Ax + Bx)/2 ; (Ay + By)/2)
M((-3 + -4)/2 ; (9 + 8)/2)
M(-3,5 ; 8,5)
г) Посчитаем длину каждой стороны треугольника
AB = 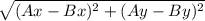 =
= 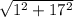 =
= 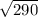
AC = 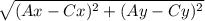 =
= 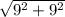 =
= 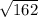
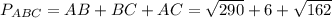
д) СМ = 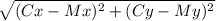 =
= 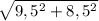 =
= 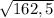
![\sqrt[n]{x}](/tpl/images/0258/0436/b773b.png)
По формулі площі
Объяснение:
Площа прямокутного трикутника дорівнює півдобутку його катетів
S = ab/2
S = (9 * 10) / 2 = 90/2 = 45
Відповідь: 45 см²