92 см
Объяснение:
Нада піднести катети до другої степеню і додати а потім дане чило під корінь і вирахувати
Четырёхугольник ABCD вписан в окружность.
∠В : ∠D = 1 : 5
∠A < в 2 раза ∠С.
Найти:∠А - ? ; ∠В - ? ; ∠С - ? ; ∠D - ? .
Решение:Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
Около четырёхугольника ABCD описана окружность, по условию ⇒ ∠B + ∠D = 180˚; ∠A + ∠C = 180°.
Найдём ∠B и ∠D:
Пусть х - ∠В, тогда 5х - ∠D. (∠B : ∠D = 1 : 5, по условию)
Как я написала ранее, ∠B + ∠D = 180˚, по свойству.
х + 5х = 180
6х = 180
х = 30
30° - ∠B.
⇒ ∠D = 30˚ * 5 = 150˚.
Найдём ∠А и ∠С:
Пусть х - ∠А, тогда 2х - ∠С.
Как я написала ранее, ∠А + ∠С = 180°, по свойству.
х + 2х = 180
3х = 180
х = 60
60° - ∠А.
⇒ ∠С = 60° * 2 = 120°
ответ: 30°; 150°; 60°; 120°.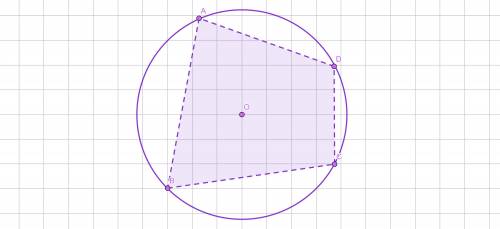
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис.2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Объяснение:
Відповідь:
Якщо трикутник прямокутний,то застосовуємо т.Піфагора. Гіпотенуза = √27² + √88² = √8473
Пояснення: