1) и 2) ответы на теоретические вопросы даются в учебниках.
3. Даны вершины тетраэдра: A(2; -1; 3), B(1; -3; 5), C(6; 2; 5), D(3; -2; - 5). Определить длину высоты от вершины D до плоскости ABC.
Находим нормальный вектор плоскости АВС.
Находим векторы АB и АC.
Вектор АВ = (1-2; -3-(-1); 5-3) = (-1; -2; 2).
Вектор АC = (6-2; 2-(-1); 5-3) = (4; 3; 2).
Нормальный вектор плоскости АBC находим из векторного произведения векторов АB и АC с применением схемы Саррюса.
i j k| i j
-1 -2 2| -1 -2
4 3 2| 4 3 = -4i + 8j - 3k + 2j - 6i + 8k =
= -10i + 10j + 5k.
Нормальный вектор плоскости АBC равен (-10; 10; 5).
Площадь треугольника АВС равна половине модуля векторного произведения векторов АВ и АС.
S = (1/2)√((-10)² + 10² + 5²) = (1*2)√(100 + 100 + 25) = (1/2)√225= (15/2) кв. ед.
Далее находим объём пирамиды ABCD.
Объём пирамиды равен 1/6 модуля смешанного произведения векторов (ABxAC)*AD.
Произведение векторов (ABxAC) найдено выше и равно (-10; 10; 5).
Находим вектор AD, точки A(2; -1; 3), D(3; -2; - 5).
AD = (3-2; -2-(-1); -5-3) = (1; -1; -8),
(ABxAC) = -10 10 5
AD = 1 -1 -8
-10 - 10 - 4 = -60.
V = (1/6)*|-60| = 10.
Длину высоты Н из точки D на плоскость АВС находим по формуле:
H = 3V/S = (3*10/(15/2) = 60/15 = 4.
Дано:
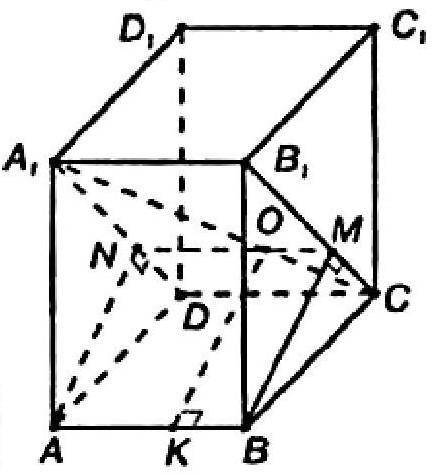
ABCDA₁B₁C₁D₁ - правильная четырехугольная призма
BC = 15 см
BB₁ = 20 см
-------------------------------------------------------------------------------------
Найти:
OK - ?
Проведем плоскость А₁В₁СD, а через ребро АВ проведем плоскость ABMN, перпендикулярную плоскости A₁B₁CD.
Так как АВ перпендикулярна боковым граням, то ABMN - прямоугольник.
Пусть О — точка пересечения АС и MN. Проведем ОК⊥АВ. Тогда ОК = ВМ.
Так как ΔВВ₁С - прямоугольный (∠B₁BC = 90°), тогда используется во теореме Пифагора:
B₁C² = BB₁² + BC² ⇒ B₁C = √BB₁² + BC² - теорема Пифагора
B₁C = √(20 см)² + (15 см)² = √400 см² + 225 см² = √625 см² = 25 см
Далее мы находим площадь ΔВВ₁С по формуле Герона:
S(ΔВВ₁С) = √p(p-BC)(p-BB₁)(p-B₁C) - Формула Герона
p = BC+BB₁+B₁C/2 = 15 см + 20 см + 25 см / 2 = 60 см/2 = 30 см
S(ΔВВ₁С) = √30 см × (30 см - 15 см)×(30 см - 20 см)×(30 см - 25 см) = √30 см × 15 см × 10 см × 5 см = √22500 см⁴ = 150 см²
Далее мы воспользуемся площадью треугольника ВВ₁С по такой формуле:
S(ΔВВ₁С) = 1/2 × B₁C × BM - площадь треугольника
Следовательно по такой формуле мы находим высоту BM:
BM = 2S(ΔВВ₁С)/B₁C = 2×150 см²/25 см = 300 см²/25 см = 12 см ⇒ OK = BM = 12 см
ответ: OK = 12 см
P.S. Рисунок показан внизу↓
20
Объяснение:
3*(-1)+(-4)*3+5*7=-3-12+35=20