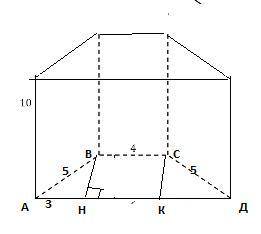
В основе прямой призмы лежит равнобедренная трапеция с основаниями 4см и 10 см и боковой стороной 5 см. Боковое ребро призмы равно 10 см. Вычислите полную поверхность призмы.
Объяснение:
В прямой призме боковое ребро перпендикулярно площади основания.
S( полной)=S(боковой)+2S(основания);
S(боковой)=Р(основания)*h, где h-ребро боковое призмы;
S(основания)=S(трапеции)=1/2*(а+в)*h ,где h-высота трапеции
S(боковой)=(4+10+2*5)*10=240 (см²).
АВСД-равнобедренная трапеция АВ=СД=5 см ; пусть ВН⊥АД, СК⊥АД ⇒ АН=(10-4):2=3 (см)
ΔАВН-прямоугольный , по т. Пифагора ВН=√(5²-3²)=4 (см).
S(трапеции)=1/2*(4+10)*4=28(см²)
S( полной)=240+2*28=296(см²)
Відповідь:
108см²
Пояснення:
Трикутник АВС- рівнобедрений сторони АВ=ВС=15СМ І ЗВІСНО ТРИКУТНИК АВО=СОВ По теоремі Піфагора сторона АО=15²-9²=
225-81=144
сторна АО=12СМ=ОС
Площа трикутника дорівнює
0,5аh=0,5·9·12=54см²
Sтрикутника АВС=54см²+54см²=108см²