! Ур-я окружности имеет общий вид :
(x-x₀)²+(y-y₀)²=R², где (х₀;у₀)- координаты центра, R- длина радиуса окр-сти.
1) Найдём координаты центра, применив формулы середины отрезка(! каждая координата середины отрезка равна полусумме коодинат его концов):
х₀=(х₁+х₂)/2=(1+4)/2=2,5
y₀=(у₁+у₂)/2= (0,5+0)/2=0,25-
2) Вычисмлим радиус как половину диаметра, а диаметр найдём по ф-ле расстояния между двумя точками:
R=D/2=(√(1-4)²+(0,5-0)²)/2=√9,25/2
3)Таким образом ,ур-е окр-сти имеет вид (х -2,5)²+(y-0,25)²= (√9,25/2)²
(х -2,5)²+(y-0,25)²= 9,25/4
(х -2,5)²+(y-0,25)²= 2,3125
! Площадь бок. поверхности прав. пирамиды равна произведению половины периметра основания на апофему, т.е.
S бок= 0,5·Р осн·SM
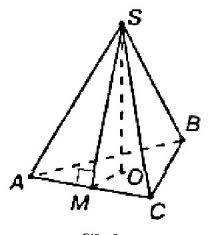
1)По условию SO=√6,SA=3√2.
Из Δ АОS-прямоуг.: АО=√АS²-SO²=√(3√2)²-(√6)²=√18-6=√12.
2) Из Δ АВС-правильный: АО- радиус описанной окружности.!Сторона правильного тр-ка равна произведению радиуса описанной окружности на √3, т.е.
АС=АО·√3=√12·√3=√36=6, тогда Р = 3·6=18.
3) найдём апофему SM из прям. тр-ка АМS:
SM= √AS²-AM²=√(3√2)²-3²=√18-9=√9=3 .
4) S бок= 0,5·Р осн·SM= 0,5·18·3=27 (кв.ед.)
600
Объяснение:
Пусть меньшая диагональ d1 = 5х, высота h = 4х, сторона ромба -а
p=4a, а=100/4=25
S=a*h=25*4x
S=1/2*d1*d2
по т. Пифагора
d2=2*sqrt(25^2 - (25/4*x^2))
Чтобы избавиться от корня возведем уравнения площадей ромба в квадрат и приравняем. Получится:
25^2 * 4^2 * x^2 = 4/4 *25* x^2 * (25^2 - (25/4*x^2))
25^2 * 4^2 * x^2 = 25^3 * x^2 - (25^2 *x^4)/4 | *(4/(25^2 * x^2))
4^3 = 100 - x^2
x^2 = 36
x=6
S=a*h=25*4x = 25 * 4 * 6=600