Чертёж смотрите во вложении.
Дано:ΔАВС - прямоугольный.
∠А = 90°.
∠С = 30°.
Точка М - середина СВ.
МН - серединный перпендикуляр.
Доказать:МН < больший катет (АС) в 3 раза.
Доказательство:Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно -
∠С+∠В = 90°
∠В = 90°-∠С
∠В = 90°-30°
∠В = 60°.
Проведём медиану к гипотенузе. Она пересечёт точку М, так как эта точка середина по условию.
Медиана, проведённая к гипотенузе, делит прямоугольный треугольник на два равнобедренных треугольника (так как медиана, проведённая к гипотенузе, равна её половине).
То есть -
ΔАСМ и ΔАМВ - равнобедренные.
Рассмотрим ΔАМВ - равнобедренный. У него есть угол в 60°, а значит, он и равносторонний (признак равностороннего треугольника).
Следовательно, по свойству равностороннего треугольника, ∠АМВ = 60° (каждый угол равностороннего треугольника равен по 60°).
Рассмотрим ΔАСМ - равнобедренный. ∠С = ∠МАС = 30° (так как углы у основания равнобедренного треугольника равны.
Рассмотрим ∠НМВ = 90°.
∠НМВ = ∠НМА+∠АМВ
∠НМА = ∠НМВ-∠АМВ
∠НМА = 90°-60°
∠НМА = 30°.
Так как ∠НМА = ∠НАМ, то ΔАНМ - равнобедренный (по признаку равнобедренного треугольника. Причём НМ = АН (так как лежат против равных углов в одном треугольнике).
Рассмотрим ΔСНМ - прямоугольный. Пусть катет НМ - х.
Против угла в 30° лежит катет, равный половине гипотенузе.
То есть -
СН = 2*НМ
СН = 2х.
Но НМ = АН = х (по выше доказанному).
Поэтому -
АС = СН+АН
АС = 2х+х
АС = 3х.
А теперь составим отношение АС и НМ, и сравним их -
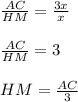
Это нам и нужно было доказать.
ответ:что требовалось доказать.

Пусть М – середина гипотенузы AB прямоугольного треугольника ABC, угол A = 30°, K – такая точка катета AC, для которой KM перпендикулярно AB. Тогда KM = 1/2 AK.
Так как CM = 1/2 AB = MB, то треугольник CMK – равнобедренный, а так как угол MBC = 60°, то этот треугольник равносторонний. Поэтому
угол KMC = 30° = углу KCM.
Следовательно, треугольник CKM – равнобедренный. Значит, CK = KM = 1/3 AC.
Извини, я не могу прикрепить чертеж, так как сижу за компом, но там надо всего лишь нарисовать прям. треугольник и обозначить углы.
Объяснение:
Дано:
ABCD - параллелограмм.
∠ABC = ∠ADC = 150°
AB = CD = 9 см
BC = AD = 10 см
Найти: S параллелограмма ABCD
∠BAD = ∠BCD = (360° - ∠ABC - ∠ADC) ÷ 2 =
= (360° - 150° - 150°) ÷ 2 = 60° ÷ 2 = 30° (сумма углов параллелограмма равна 360°)
Опустим высоту BE
Рассмотрим прямоугольный треугольник ABE:
∠A = 30° ⇒ BE = 1/2AB = 4,5 см (в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы)
S параллелограмма ABCD = AD × BE = 10 × 4,5 = 45 см² (площадь параллелограмма равна произведению его стороны на высоту опущенную к этой стороне)
ответ: 45 см²
№2Рассмотрим треугольник CDE:
∠C = 180° - ∠D - ∠E =
= 180° - 45° - 90° = 45° (сумма углов треугольника равна 180°)
∠C = ∠D ⇒ ΔCDE равнобедренный ⇒
⇒ CE = DE = 4 см
Рассмотрим прямоугольный треугольник CBF:
∠B = 180° - 90° - 60° = 30° (сумма углов треугольника равна 180°)
Пусть AF = x
Тогда AB = 2x (в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы)
Найдём x:
x² + 4² = (2x)² (теорема Пифагора)
16 = 4x² - x²
3x² = 16
x² = 16/3
x = 4/√3 = (4√3)/3 см = AF
FE = BC = 3 см
AD = AF + FE + DE = (4√3)/3 + 3 + 4 =
= (4√3)/3 + 7/1 = (4√3 + 21)/3
S трапеции ABCD = (AD + BC)/2 × CE =
= ((4√3 + 21)/3 + 3)/2 × 4 =
= (4√3 + 30)/3 × 2 = (8√3 + 60)/3 (площадь трапеции равна полусумме оснований умноженной на высоту)
ответ: (8√3 + 60)/3
№3 (чертёж прилагается)Дано:
ABCD - ромб со стороной 15 см
AC = 24 см
Найти: S ромба ABCD
Проведём вторую диагональ.
Диагонали ромба делят друг друга пополам ⇒
⇒ AE = CE = 1/2 AC = 24 ÷ 2 = 12 см
Рассмотрим прямоугольный треугольник ABE:
BE = DE = √(AB² - AE²) = √(225 - 144) =
= √81 = 9 см (теорема Пифагора)
BD = BE + DE = 9 + 9 = 18 см
S ромба ABCD = (AC × BD)/2 =
= (24 × 18)/2 = 24 × 9 = 216 см² (площадь ромба равна половине произведения его диагоналей)
ответ: 216 см²