Пусть расстояние от вершины одного острого угла до точки касания равно х
Тогда один катет равен
х+2
Второй
17-х-2
Гипотенуза равна сумме отрезков от острых углов треугольника до точек касания с окружностью по свойству касательных из одной точки к окружности.
х+ 17-х-2-2=13cм
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов:
(17 -х)²+х²=13²
289-34х+х²+х²=169
2х²-34х +120=0
D = b² - 4ac = 196
х1=5 см
х2=12 см
Один катет равен 5, второй 12
Площадь равна половине произведения катетов и равна
5*12:2=30 см²
Проверка
5²+12²=169
169=169
√169=13
1. ΔABC-правильный . R и r-радиусы вписанной и описанной окружностей. Выразите R через r.
a₃ = 2r√3 и a₃ = R√3 ⇒ 2r√3= R√3 , R=2r.
4. Найдите площадь равностороннего треугольника, вокруг которого описано окружность радиуса 3 см.
a₃ = R√3 ⇒ a₃ = 3√3 см
S(равностороннего треуг.)=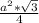
⇒ S(равн.треуг.)= 
= 
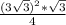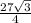(cм²)
5. Определите количество сторон правильного многоугольника углы которого равны 160 градусов.
Многоугольник правильный , поэтому сумма всех внутренних углов 160*n .
160*n=180(n-2) , 160n=180n-360 , 20n=360 , n=18. Количество сторон 18.
((n-2)/n*180- формула для нахождения углов в правильном многоугольнике )
6. В правильный треугольник ,сторона которого 4√3 cм, вписана окружность. Вокруг окружности описан квадрат. Найдите сторону квадрата.
a₃ = 2r√3 , 4√3= 2r√3 ⇒ r=2 см.
Квадрат описан около окружности, значит сторона квадрата равна
a₄ =2r или a₄ =4см.