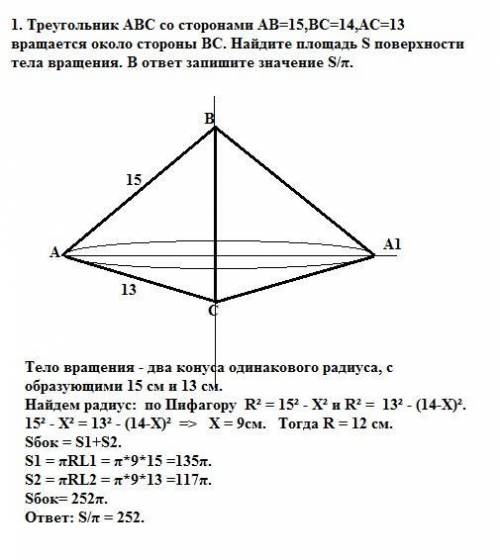
1. Тело вращения - два конуса одинакового радиуса, с образующими 15 см и 13 см.
Найдем радиус: по Пифагору R² = 15² - Х² (1) и R² = 13² - (14-Х)² (2).
Приравняем (1) и (2).
15² - Х² = 13² - (14-Х)² => X = 9см. Тогда R = 12 см.
Sбок = S1+S2.
S1 = πRL1 = π*9*15 =135π.
S2 = πRL2 = π*9*13 =117π.
Sбок= 252π.
ответ: S/π = 252.
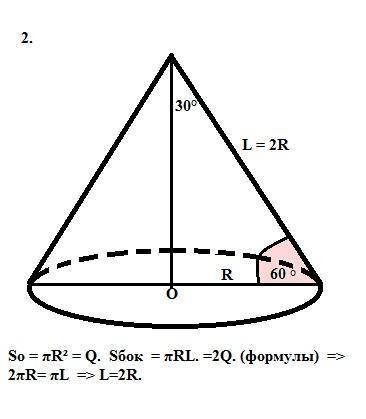
2. Площадь основания конуса - Q, а площадь боковой поверхности - 2Q. Под каким углом его образующая наклонена к плоскости основания?
So = πR² = Q. Sбок = πRL. =2Q. (формулы) => 2πR= πL => L=2R.
Образующая (гипотенуза) в 2 раза больше радиуса.
Значит угол против радиуса в осевом сечении конуса равен 30°, а угол между образующей и плоскостью основания = 60°.
ответ: угол равен 60°
81 см²
Объяснение:
По умові:
AM = 2/9 * AC
AK = 2/9 * AB
Розглянемо ΔAMK і ΔABC:
∠A - спільний
AM = 2/9 * AC
AK = 2/9 * AB
Один кут рівний і пропорційні дві прилеглі до нього сторони. Це ознака подібності трикутників:
ΔAMK ~ ΔACB (k = 2/9)
Тоді:
MK = BC * k = BC * 2/9
BC = MK / (2/9) = 18 / (2/9) = (18 * 9) / 2 = 9 * 9 = 81
Відповідь: 81 см²