A1. Две прямые на плоскости называются параллельными, если они:
4) не пересекаются
А2. Один из признаков параллельности двух прямых гласит:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А3. Выберите утверждение, являющееся аксиомой параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
А4. Если две параллельные прямые пересечены секущей, то:
Соответственные углы равны
А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:
Она перпендикулярна и другой
А6. Всякая теорема состоит из нескольких частей:
Условия и заключения
А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:
Накрест лежащие, соответственные, односторонние
А8. Аксиома – это:
Положение геометрии, не требующее доказательства
А9. Выберите утверждение, которое является признаком параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А10. Если прямая не пересекает одну из двух параллельных прямых, то:
Другую прямую она тоже не пересекает
или
С другой прямой она совпадает
ответ: 864 см³
Объяснение:
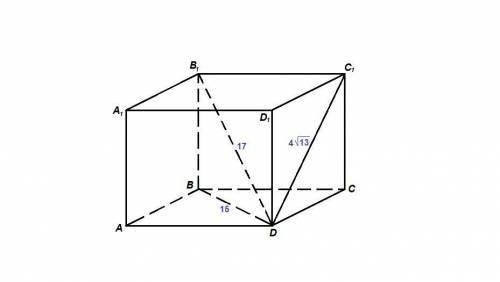
Все грани прямоугольного параллелепипеда - прямоугольники, диагонали прямоугольника равны, поэтому
АС = BD = 15 см
Объем прямоугольного параллелепипеда равен произведению трех его измерений. Найдем их.
ΔВ₁BD: ∠B₁BD = 90°, по теореме Пифагора:
ВВ₁ = √(DB₁² - BD²) = √(17² - 15²) = √((17 - 15)(17 + 15)) =
= √(2 · 32) = 64 = 8 см
СС₁ = ВВ₁ = 8 см
ΔDCC₁: ∠DCC₁ = 90°, по теореме Пифагора:
CD = √(DC₁² - CC₁²) = √((4√13)² - 8²) = √(208 - 64) = √144 = 12 см
ΔBCD: ∠BCD = 90°, по теореме Пифагора:
BC = √(BD² - CD²) = √(15² - 12²) = √((15 - 12)(15 + 12)) =
= √(3 · 27) = √81 = 9 см
V = CD · BC · BB₁ = 12 · 9 · 8 = 864 см³
скорее всего та Которая 5 см, потому что у любого равнобедренного треугольника две одинаковые стороны, а пять самая большая