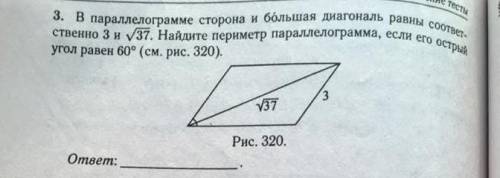
По теореме косинусов квадрат большей диагонали равен сумме квадратов смежных сторон без удвоенного произведения этих сторон на косинус 120 градусов, т.к. сумма углов, прилежащей к стороне 3, равна 180 градусов. т.е. тупой угол между смежными сторонами равен 120°, пусть неизвестная сторона, смежная стороне 3, равна х, тогда, учитав, что косинус 120 градусов равен -0.5, получим
37=9+х²-2*3*х*(-0.5)
х²+3х-28=0
х=(-3±√(9+112))/2=(-3±11)/2; х=-7; ∅, сторона не бывает отрицательной. Значит х=4, тогда периметр 2*(3+4)=14
ответ 14
1) Проведем медиану AP, ⇒ CP = PB.
2) AO:OP = 2:1 (по свойству пересекаемых медиан)
3) ΔCOB — прямоугольный, т.к. CO⊥BO (CO∈CK, BO∈BE, CK⊥BE по условия задачи)
4) OP — медиана ΔCOB, т.к. ΔCOB — прямоугольный, CP = PB, а медиана делит сторону, на которую опущена, только в прямоугольном треугольнике, и эта сторона — гипотенуза, а угол, с которого проведена медиана — прямой.
Следовательно, OP = 1/2CB, или OP:CB = 1:2
5) AP:CB = (AO+OP):CB = (2+1):2 = 3:2.
ответ: отношение третьей медианы к соответствующий стороне — 3:2.
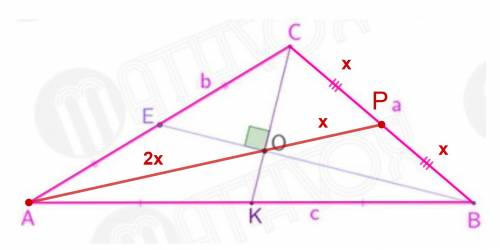
1) Проведем медиану AP, ⇒ CP = PB.
2) AO:OP = 2:1 (по свойству пересекаемых медиан)
3) ΔCOB — прямоугольный, т.к. CO⊥BO (CO∈CK, BO∈BE, CK⊥BE по условия задачи)
4) OP — медиана ΔCOB, т.к. ΔCOB — прямоугольный, CP = PB, а медиана делит сторону, на которую опущена, только в прямоугольном треугольнике, и эта сторона — гипотенуза, а угол, с которого проведена медиана — прямой.
Следовательно, OP = 1/2CB, или OP:CB = 1:2
5) AP:CB = (AO+OP):CB = (2+1):2 = 3:2.
ответ: отношение третьей медианы к соответствующий стороне — 3:2.

ответ: Асса
Объяснение: